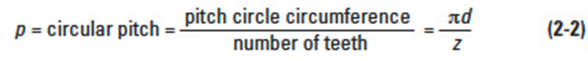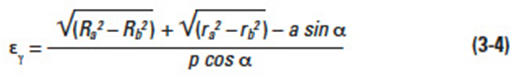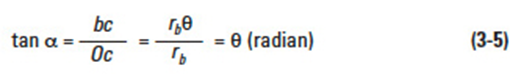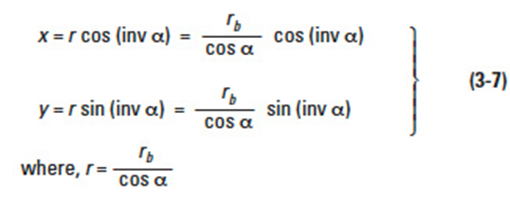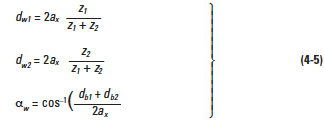Gears sections 1 - 4
Gears are some of the most important elements used in machinery. There are few mechanical devices that do not have the need to transmit power and motion between rotating shafts. Gears not only do this most satisfactorily, but can do so with uniform motion and reliability. In addition, they span the entire range of applications from large to small. To summarize:
- Gears offer positive transmission of power.
- Gears range in size from small miniature instrument installations, that measure in only several millimeters in diameter, to huge powerful gears in turbine drives that are several meters in diameter.
- Gears can provide position transmission with very high angular or linear accuracy; such as used in servomechanisms and military equipment.
- Gears can couple power and motion between shafts whose axes are parallel, intersecting or skew.
- Gear designs are standardized in accordance with size and shape which provides for widespread interchangeability
Section 1: Introduction to metric gearsEdit
1.1 Comparison Of Metric Gears With American Inch GearsEdit
1.1.1 Comparison of Basic RacksEdit
In all modern gear systems, the rack is the basis for tooth design and manufacturing tooling. Thus, the similarities and differences between the two systems can be put into proper perspective with comparison of the metric and inch basic racks.
In both systems, the basic rack is normalized for a unit size. For the metric rack it is 1 module, and for the inch rack it is 1 diametral pitch.
1.1.2 Metric ISO Basic RackEdit
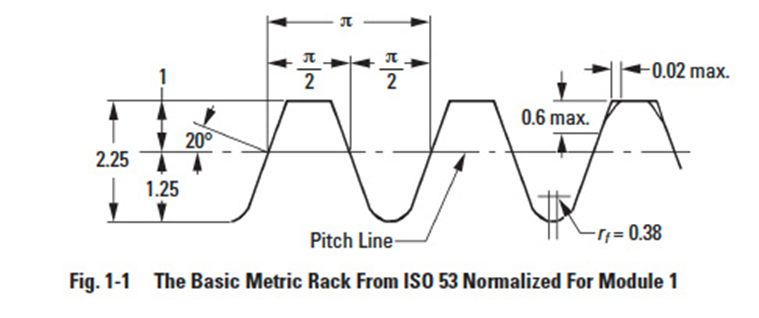
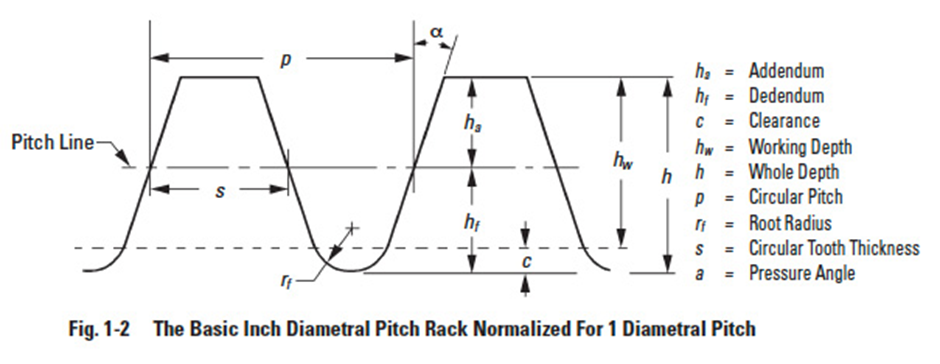
The standard ISO metric rack is detailed in Figure 1-1. It is now the accepted standard for the international community, it having eliminated a number of minor differences that existed between the earlier versions of Japanese, German and Russian modules. For comparison, the standard inch rack is detailed in Figure 1-2. Note that there are many similarities. The principal factors are the same for both racks. Both are normalized for unity; that is, the metric rack is specified in terms of 1 module, and the inch rack in terms of 1 diametral pitch.
From the normalized metric rack, corresponding dimensions for any module are obtained by multiplying each rack dimension by the value of the specific module m. The major tooth parameters are defined by the standard, as:
- Tooth Form:Straight-sided full depth, forming the basis of a family of full depth interchangeable gears.
- Pressure Angle:A 20° pressure angle, which conforms to worldwide acceptance of this as the most versatile pressure angle.
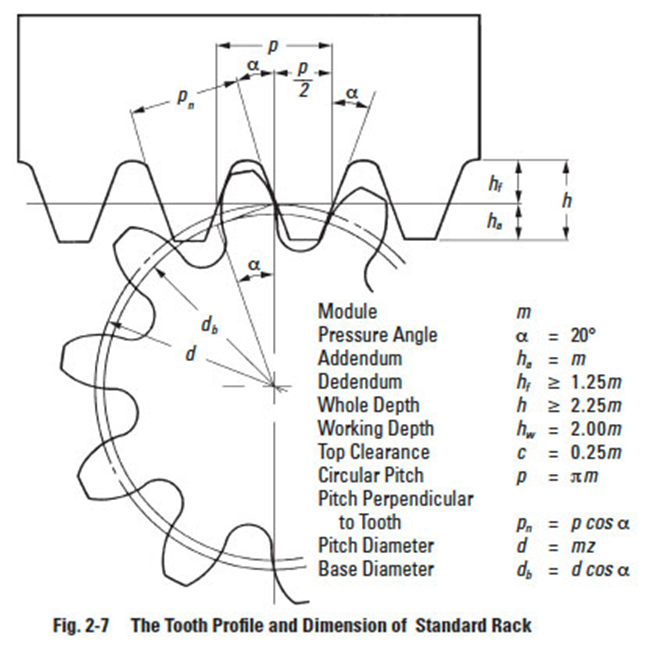
- Addendum:This is equal to the module m, which is similar to the inch value that becomes 1/p.
- Dedendum:This is 1.25 m; again similar to the inch rack value.
- Root Radius:The metric rack value is slightly greater than the American inch rack value.
- Tip Radius:A maximum value is specified. This is a deviation from the American inch rack which does not specify a rounding.
1.2 Metric Standards WorldwideEdit
1.2.1 ISO StandardsEdit
Metric standards have been coordinated and standardized by the International Standards Organization (ISO). A listing of the most pertinent standards is given in Table 1-1.
1.2.2 Foreign Metric StandardsEdit
Most major industrialized countries have been using metric gears for a long time and consequently had developed their own standards prior to the establishment of ISO and SI units. In general, they are very similar to the ISO standards. The key foreign metric standards for Australia and France, Germany, Italy and Japan are in the appendix. United Kingdom is shown above.
1.3.3 TerminologyEdit
Terms used in metric gearing are identical or are parallel to those used for inch gearing. The one major exception is that metric gears are based upon the module, which for reference may be considered as the inversion of a metric unit diametral pitch.
Section 2: introduction to gear technologyEdit
This section presents a technical coverage of gear fundamentals. It is intended as a broad coverage written in a manner that is easy to follow and to understand by anyone interested in knowing how gear systems function. Since gearing involves speciality components, it is expected that not all designers and engineers possess or have been exposed to every aspect of this subject. However, for proper use of gear components and design of gear systems it is essential to have a minimum understanding of gear basics and a reference source for details.
2.1 Basic Geometry Of Spur GearsEdit
The fundamentals of gearing are illustrated through the spur gear tooth, both because it is the simplest, and hence most comprehensible, and because it is the form most widely used, particularly for instruments and control systems.
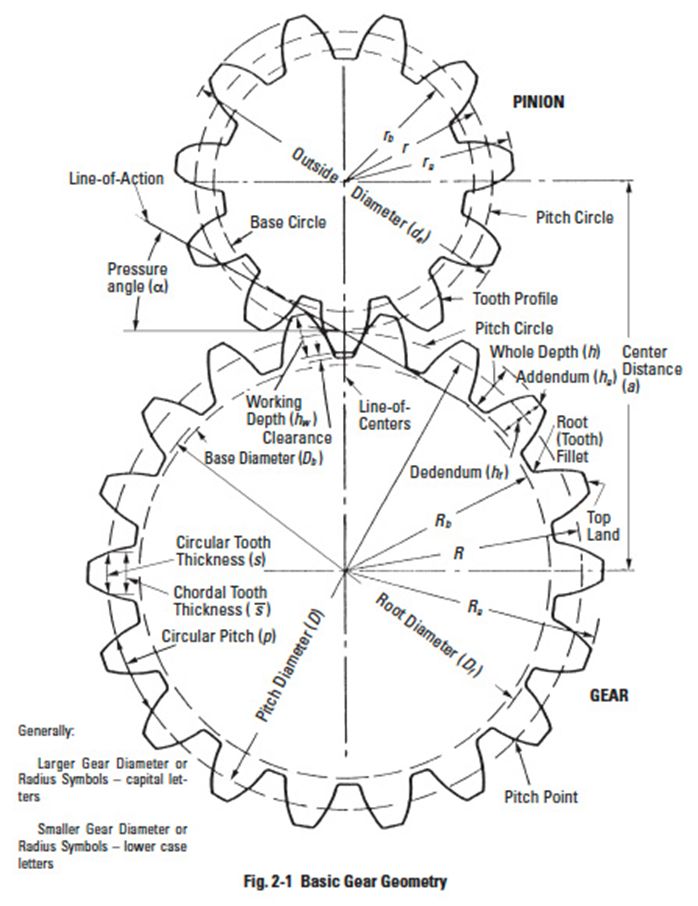
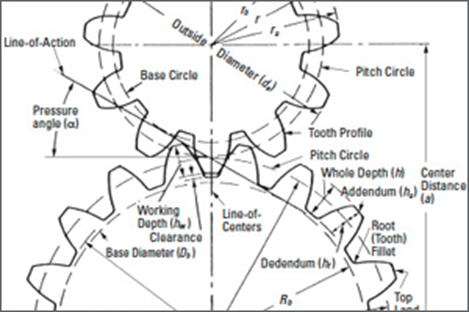
The basic geometry and nomenclature of a spur gear mesh is shown in Figure 2-1. The essential features of a gear mesh are:
- Centre distance.
- The pitch circlediameters (or pitch diameters).
- Size of teeth (or module).
- Number of teeth.
- Pressure angle of the contacting involutes
Details of these items along with their interdependence and definitions are covered in subsequent paragraphs.
2.2 The Law Of GearingEdit
A primary requirement of gears is the constancy of angular velocities or proportionality of position transmission. Precision instruments require positioning fidelity. High-speed and/or high-power gear trains also require transmission at constant angular velocities in order to avoid severe dynamic problems.
Constant velocity (i.e., constant ratio) motion transmission is defined as "conjugate action" of the gear tooth profiles. A geometric relationship can be derived (2, 12)* for the form of the tooth profiles to provide conjugate action, which is summarized as the Law of Gearing as follows:
"A common normal to the tooth profiles at their point of contact must, in all positions of the contacting teeth, pass through a fixed point on the line-of-centres called the pitch point." Any two curves or profiles engaging each other and satisfying the law of gearing are conjugate curves.
2.3 The Involute CurveEdit
There is almost an infinite number of curves that can be developed to satisfy the law of gearing, and many different curve forms have been tried in the past. Modern gearing (except for clock gears) is based on involute teeth. This is due to three major advantages of the involute curve:
- Conjugate action is independent of changes in centre distance.
- The form of the basic rack tooth is straight-sided, and therefore is relatively simple and can be accurately made; as a generating tool it imparts high accuracy to the cut gear tooth.
- One cutter can generate all gear teeth numbers of the same pitch.
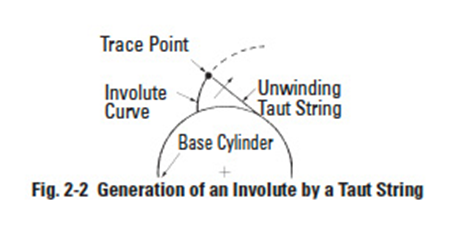
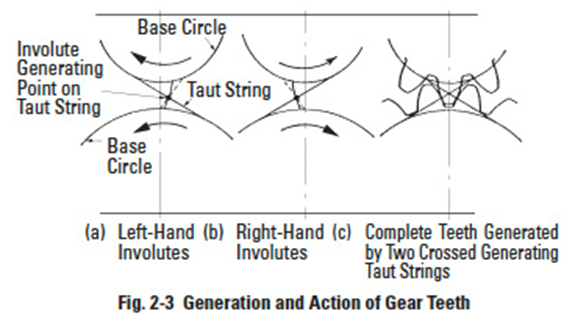
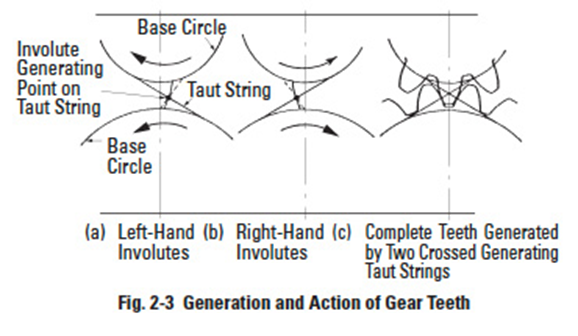
The involute curve is most easily understood as the trace of a point at the end of a taut string that unwinds from a cylinder. It is imagined that a point on a string, which is pulled taut in a fixed direction, projects its trace onto a plane that rotates with the base circle. See Figure 2-2. The base cylinder, or base circle as referred to in gear literature, fully defines the form of the involute and in a gear it is an inherent parameter, though invisible.
The development and action of mating teeth can be visualized by imagining the taut string as being unwound from one base circle and wound on to the other, as shown in a Figure 2-3a. Thus, a single point on the string simultaneously traces an involute on each base circle's rotating plane. This pair of involutes is conjugate, since at all points of contact the common normal is the common tangent which passes through a fixed point on the line-of-centers. If a second winding/ unwinding taut string is wound around the base circles in the opposite direction, Figure 2-3b, oppositely curved involutes are generated which can accommodate motion reversal. When the involute pairs are properly spaced, the result is the involute gear tooth, Figure 2-3c.
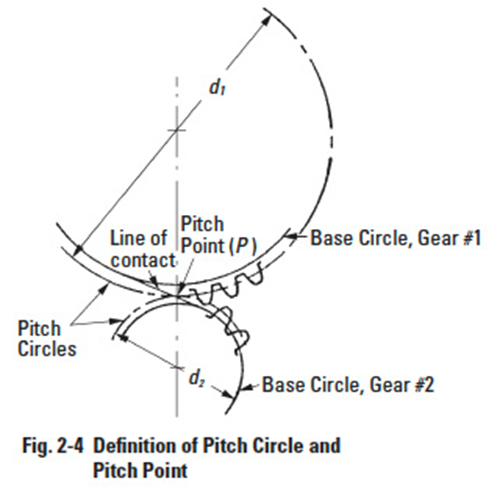
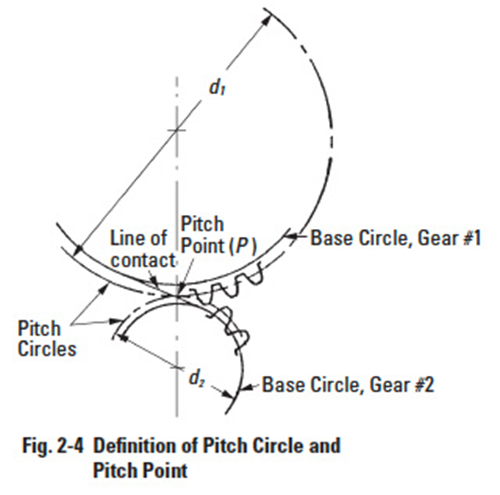
2.4 Pitch CirclesEdit
Referring to Figure 2-4, the tangent to the two base circles is the line of contact, or line-of-action in gear vernacular. Where this line crosses the line-of-centres establishes the pitch point, P. This in turn sets the size of the pitch circles, or as commonly called, the pitch diameters. The ratio of the pitch diameters gives the velocity ratio:
Velocity ratio of gear 2 to gear 1 is:
2.5 Pitch And ModuleEdit
Essential to prescribing gear geometry is the size, or spacing of the teeth along the pitch circle. This is termed pitch, and there are two basic forms.
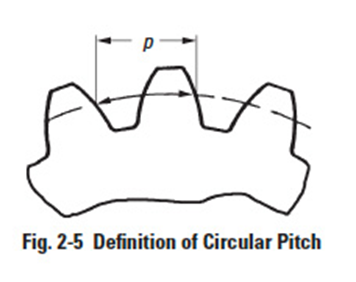
Circular pitch — A naturally conceived linear measure along the pitch circle of the tooth spacing. Referring to Figure 2-5, it is the linear distance (measured along the pitch circle arc) between corresponding points of adjacent teeth. It is equal to the pitch-circle circumference divided by the number of teeth:
Module— Metric gearing uses the quantity module m in place of the American inch unit, diametral pitch. The module is the length of pitch diameter per tooth. Thus:
Relation of pitches: From the geometry that defines the two pitches, it can be shown that module and circular pitch are related by the expression:
This relationship is simple to remember and permits an easy transformation from one to the other.
Diametral pitch is widely used in England and America to represent the tooth size. The relation between diametral pitch and module is as follows:
2.6 Module Sizes And StandardsEdit
Module m represents the size of involute gear tooth. The unit of module is mm. Module is converted to circular pitch p, by the factor π.
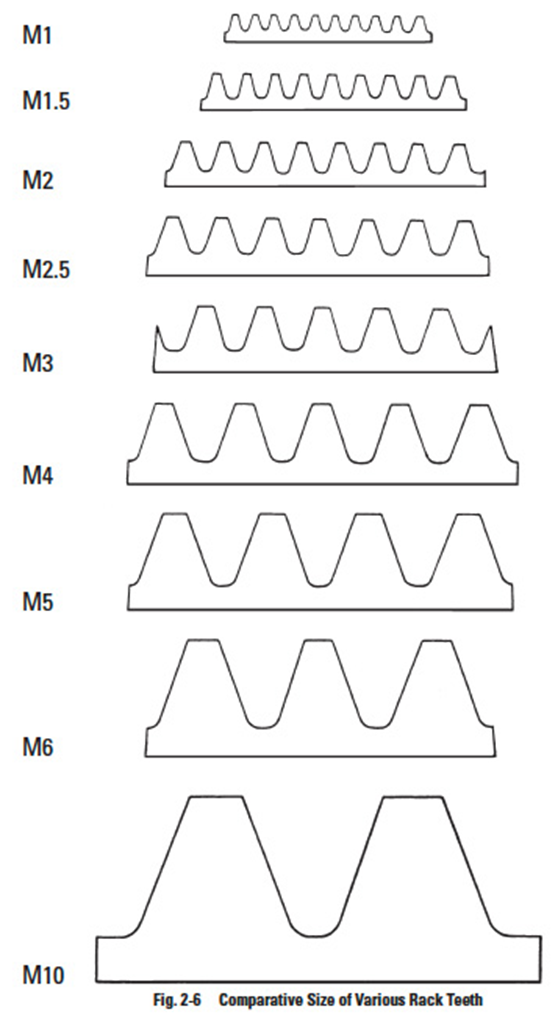
Figure 2-6 shows the comparative size of various rack teeth.
Circular pitch, p, is also used to represent tooth size when a special desired spacing is wanted, such as to get an integral feed in a mechanism. In this case, a circular pitch is chosen that is an integer or a special fractional value. This is often the choice in designing position control systems. Another particular usage is the drive of printing plates to provide a given feed. Most involute gear teeth have the standard whole depth and a standard pressure angle α = 20°. Figure 2-7 shows the tooth profile of a whole depth standard rack tooth and mating gear. It has an addendum of = 1m and dedendum ≥ 1.25m. If tooth depth is shorter than whole depth it is called a "stub" tooth; and if deeper than whole depth it is a "high" depth tooth.
The most widely used stub tooth has an addendum = 0.8m and dedendum = 1m. Stub teeth have more strength than a whole depth gear, but contact ratio is reduced. On the other hand, a high depth tooth can increase contact ratio, but weakens the tooth.
In the standard involute gear, pitch p times the number of teeth becomes the length of pitch circle:
Gear Types and Axial Arrangements; Details of Involute Gearing
2.7 Gear Types And Axial ArrangementsEdit
In accordance with the orientation of axes, there are three categories of gears:
- Parallel Axes Gears
- Intersecting Axes Gears
- Nonparallel and Nonintersecting Axes Gears
Spur and helical gears are the parallel axes gears. Bevel gears are the intersecting axes gears. Screw or crossed helical, worm and hypoid gears handle the third category. Table 2-3 lists the gear types per axes orientation.
Also, included in Table 2-3 is the theoretical efficiency range of the various gear types. These figures do not include bearing and lubricant losses. Also, they assume ideal mounting in regard to axis orientation and center distance. Inclusion of these realistic considerations will downgrade the efficiency numbers.
2.7.1 Parallel Axes GearsEdit
Spur Gear
This is a cylindrical shaped gear in which the teeth are parallel to the axis. It has the largest applications and, also, it is the easiest to manufacture.
2. Spur Rack
This is a linear shaped gear which can mesh with a spur gear with any number of teeth. The spur rack is a portion of a spur gear with an infinite radius.
3. Internal Gear
This is a cylindrical shaped gear but with the teeth inside the circular ring. It can mesh with a spur gear. Internal gears are often used in planetary gear systems.
4. Helical Gear
This is a cylindrical shaped gear with helicoid teeth. Helical gears can bear more load than spur gears, and work more quietly. They are widely used in industry. A disadvantage is the axial thrust force the helix form causes.
5. Helical Rack
This is a linear shaped gear which meshes with a helical gear. Again, it can be regarded as a portion of a helical gear with infinite radius.
6. Double Helical Gear
This is a gear with both left-hand and right-hand helical teeth. The double helical form balances the inherent thrust forces.
2.7.2 Intersecting Axes GearsEdit
- Straight Bevel Gear
This is a gear in which the teeth have tapered conical elements that have the same direction as the pitch cone base line (generatrix). The straight bevel gear is both the simplest to produce and the most widely applied in the bevel gear family.
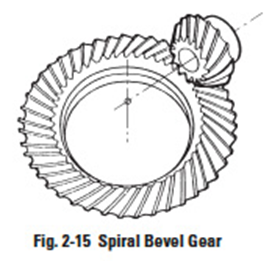
2. Spiral Bevel Gear
This is a bevel gear with a helical angle of spiral teeth. It is much more complex to manufacture, but offers a higher strength and lower noise.
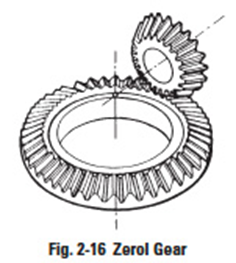
3. Zerol GearEdit
Zerol gear is a special case of spiral bevel gear. It is a spiral bevel with zero degree of spiral angle tooth advance. It has the characteristics of both the straight and spiral bevel gears. The forces acting upon the tooth are the same as for a straight bevel gear.Edit
2.7.3 Nonparallel And Nonintersecting Axes GearsEdit
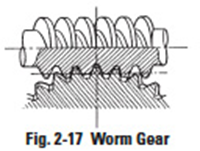
Worm And Worm Gear
Worm set is the name for a meshed worm and worm gear. The worm resembles a screw thread; and the mating worm gear a helical gear, except that it is made to envelope the worm as seen along the worm's axis. The outstanding feature is that the worm offers a very large gear ratio in a single mesh. However, transmission efficiency is very poor due to a great amount of sliding as the worm tooth engages with its mating worm gear tooth and forces rotation by pushing and sliding. With proper choices of materials and lubrication, wear can be contained and noise is reduced.
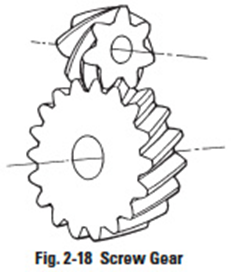
2. Screw Gear (Crossed Helical Gear)
Two helical gears of opposite helix angle will mesh if their axes are crossed. As separate gear components, they are merely conventional helical gears. Installation on crossed axes converts them to screw gears. They offer a simple means of gearing skew axes at any angle. Because they have point contact, their load carrying capacity is very limited.
2.7.4 Other Special GearsEdit
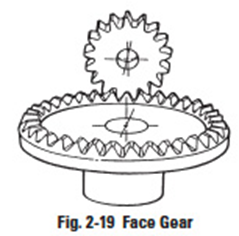
Face Gear
This is a pseudobevel gear that is limited to 90° intersecting axes. The face gear is a circular disc with a ring of teeth cut in its side face; hence the name face gear. Tooth elements are tapered towards its center. The mate is an ordinary spur gear. It offers no advantages over the standard bevel gear, except that it can be fabricated on an ordinary shaper gear generating machine.
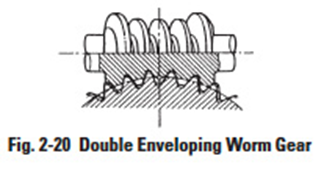
2. Double Enveloping Worm Gear
This worm set uses a special worm shape in that it partially envelops the worm gear as viewed in the direction of the worm gear axis. Its big advantage over the standard worm is much higher load capacity. However, the worm gear is very complicated to design and produce, and sources for manufacture are few.
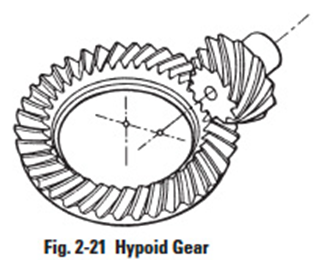
3. Hypoid Gear
This is a deviation from a bevel gear that originated as a special development for the automobile industry. This permitted the drive to the rear axle to be non intersecting, and thus allowed the auto body to be lowered. It looks very much like the spiral bevel gear. However, it is complicated to design and is the most difficult to produce on a bevel gear generator.
Section 3: Details of involute gearingEdit
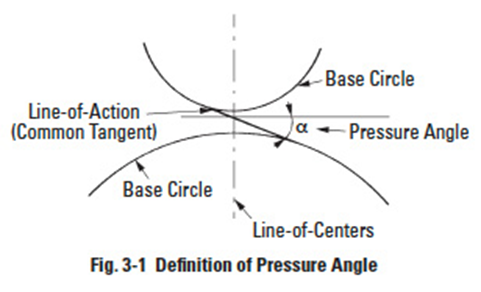
3.1 Pressure AngleEdit
The pressure angle is defined as the angle between the line-of-action (common tangent to the base circles in Figures 2-3 and 2-4) and a perpendicular to the line-of-centres. See Figure 3-1. From the geometry of these figures, it is obvious that the pressure angle varies (slightly) as the centre distance of a gear pair is altered. The base circle is related to the pressure angle and pitch diameter by the equation:
where d and α are the standard values, or alternately:
where d and α' are the exact operating value
The basic formula shows that the larger the pressure angle the smaller the base circle. Thus, for standard gears, 14.5° pressure angle gears have base circles much nearer to the roots of teeth than 20° gears. It is for this reason that 14.5° gears encounter greater undercutting problems than 20° gears. This is further elaborated on in section 4.3.
3.2 Proper Meshing And Contact RatioEdit
Figure 3-2 shows a pair of standard gears meshing together. The contact point of the two involutes, as Figure 3-2 shows, slides along the common tangent of the two base circles as rotation occurs. The common tangent is called the line-of-contact, or line-of-action.
A pair of gears can only mesh correctly if the pitches and the pressure angles are the same.
Pitch comparison can be module (m), circular (p), or base. That the pressure angles must be identical becomes obvious from the following equation for base pitch:
Thus, if the pressure angles are different, the base pitches cannot be identical.
The length of the line-of-action is shown as ab in Figure 3-2.
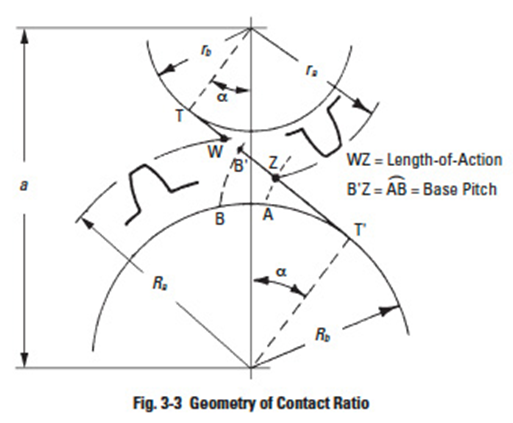
3.2.1 Contact RatioEdit
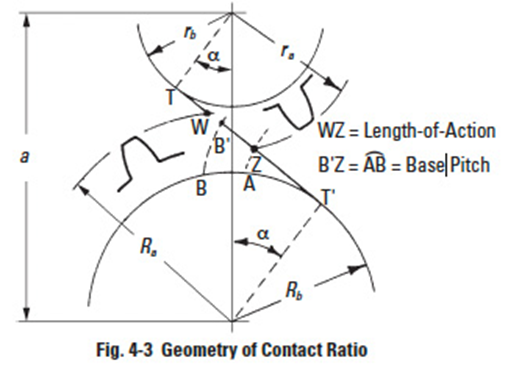
To assure smooth continuous tooth action, as one pair of teeth ceases contact a succeeding pair of teeth must already have come into engagement. It is desirable to have as much overlap as possible. The measure of this overlapping is the contact ratio. This is a ratio of the length of the line-of-action to the base pitch. Figure 3-3 shows the geometry. The length-of-action is determined from the intersection of the line-of-action and the outside radii. For the simple case of a pair of spur gears, the ratio of the length-of-action to the base pitch is determined from:
???
It is good practice to maintain a contact ratio of 1.2 or greater. Under no circumstances should the ratio drop below 1.1, calculated for all tolerances at their worst-case values.
A contact ratio between 1 and 2 means that part of the time two pairs of teeth are in contact and during the remaining time one pair is in contact. A ratio between 2 and 3 means 2 or 3 pairs of teeth are always in contact. Such a high contact ratio generally is not obtained with external spur gears, but can be developed in the meshing of an internal and external spur gear pair or specially designed non-standard external spur gears.
More detail is presented about contact ratio, including calculation equations for specific gear types, in section 11.
3.3 The Involute FunctionEdit
Figure 3-4 shows an element of involute curve. The definition of involute curve is the curve traced by a point on a straight line which rolls without slipping on the circle.
The circle is called the base circle of the involutes. Two opposite hand involute curves meeting at a cusp form a gear tooth curve. We can see, from Figure 3-4, the length of base circle arc ac equals the length of straight line bc.
The θ in Figure 3-4 can be expressed as inv α + α, then Formula (3-5) will become:
Function of α, or inv α, is known as involute function. Involute function is very important in gear design. Involute function values can be obtained from appropriate tables. With the centre of the base circle O at the origin of a coordinate system, the involute curve can be expressed by values of x and y as follows:
Section 4: Spur gear calculationsEdit
4.1 Standard Spur GearEdit
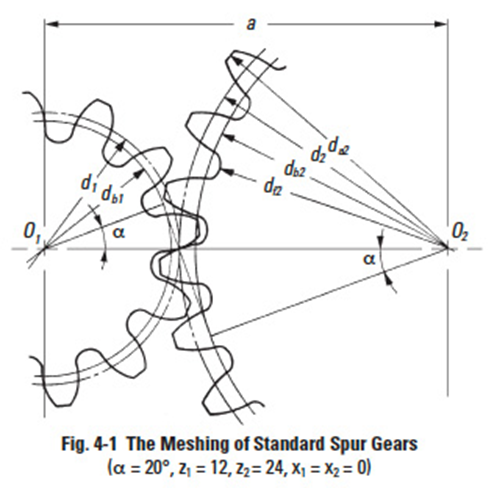
Figure 4-1 shows the meshing of standard spur gears. The meshing of standard spur gears means pitch circles of two gears contact and roll with each other. The calculation formulas are in Table 4-1.
All calculated values in Table 4-1 are based upon given module (m) and number of teeth (z1 and z2). If instead module (m), centre distance (a) and speed ratio (i) are given, then the number of teeth, z1 and z2, would be calculated with the formulas as shown in Table 4-2.
Note that the numbers of teeth probably will not be integer values by calculation with the formulas in Table 4-2. Then it is incumbent upon the designer to choose a set of integer numbers of teeth that are as close as possible to the theoretical values. This will likely result in both slightly changed gear ratio and centre distance. Should the centre distance be inviolable, it will then be necessary to resort to profile shifting. This will be discussed later in this section.
4.2 The Generating Of A Spur GearEdit
Involute gears can be readily generated by rack type cutters. The hob is in effect a rack cutter. Gear generation is also accomplished with gear type cutters using a shaper or planer machine. Figure 4-2 illustrates how an involute gear tooth profile is generated. It shows how the pitch line of a rack cutter rolling on a pitch circle generates a spur gear.
4.3 UndercuttingEdit
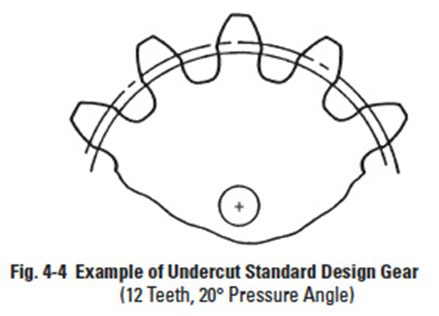
From Figure 4-3, it can be seen that the maximum length of the line-of-contact is limited to the length of the common tangent. Any tooth addendum that extends beyond the tangent points (T and T') is not only useless, but interferes with the root fillet area of the mating tooth. This results in the typical undercut tooth, shown in Figure 4-4. The undercut not only weakens the tooth with a wasp-like waist, but also removes some of the useful involute adjacent to the base circle.
From the geometry of the limiting length-of-contact (T-T', Figure 4-3), it is evident that interference is first encountered by the addenda of the gear teeth digging into the mating-pinion tooth flanks. Since addenda are standardized by a fixed value (ha= m), the interference condition becomes more severe as the number of teeth on the mating gear increases. The limit is reached when the gear becomes a rack. This is a realistic case since the hob is a rack-type cutter. The result is that standard gears with teeth numbers below a critical value are automatically undercut in the generating process. The condition for no undercutting in a standard spur gear is given by the expression:
This indicates that the minimum number of teeth free of undercutting decreases with increasing pressure angle. For 14.5° the value of zc is 32, and for 20° it is 18. Thus, 20° pressure angle gears with low numbers of teeth have the advantage of much less undercutting and, therefore, are both stronger and smoother acting
4.4 Enlarged PinionsEdit
Undercutting of pinion teeth is undesirable because of losses of strength, contact ratio and smoothness of action. The severity of these faults depends upon how far below zc the teeth number is. Undercutting for the first few numbers is small and in many applications its adverse effects can be neglected.
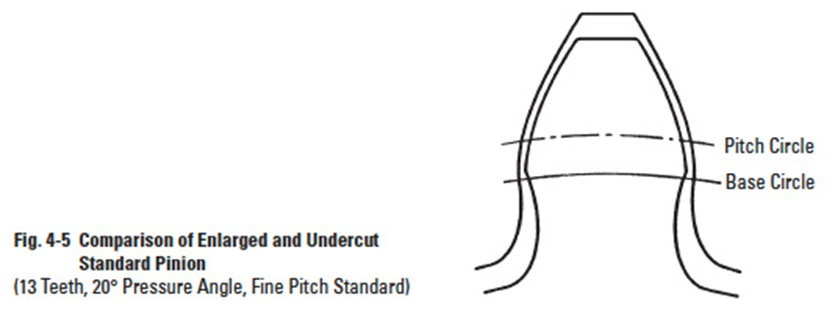
For very small numbers of teeth, such as ten and smaller, and for high-precision applications, undercutting should be avoided. This is achieved by pinion enlargement (or correction as often termed), wherein the pinion teeth, still generated with a standard cutter, are shifted radially outward to form a full involute tooth free of undercut. The tooth is enlarged both radially and circumferentially. Comparison of a tooth form before and after enlargement is shown in Figure 4-5.
4.4 Enlarged PinionsEdit
Undercutting of pinion teeth is undesirable because of losses of strength, contact ratio and smoothness of action. The severity of these faults depends upon how far below zc the teeth number is. Undercutting for the first few numbers is small and in many applications its adverse effects can be neglected.
For very small numbers of teeth, such as ten and smaller, and for high-precision applications, undercutting should be avoided. This is achieved by pinion enlargement (or correction as often termed), wherein the pinion teeth, still generated with a standard cutter, are shifted radially outward to form a full involute tooth free of undercut. The tooth is enlarged both radially and circumferentially. Comparison of a tooth form before and after enlargement is shown in Figure 4-5.
4.5 Profile ShiftingEdit
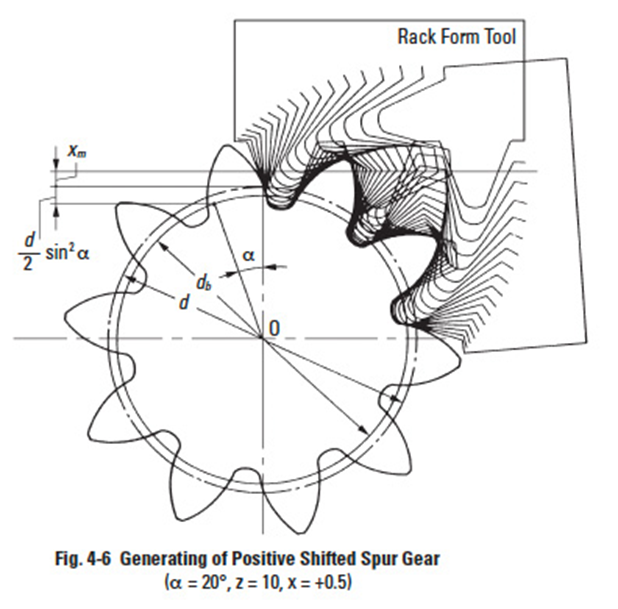
As Figure 4-2 shows, a gear with 20 degrees of pressure angle and 10 teeth will have a huge undercut volume. To prevent undercut, a positive correction must be introduced. A positive correction, as in Figure 4-6, can prevent undercut.
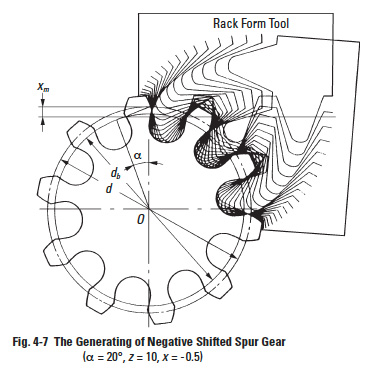
Undercutting will get worse if a negative correction is applied. See Figure 4-7. The extra feed of gear cutter (xm) in Figures 4-6 and 4-7 is the amount of shift or correction. And x is the shift coefficient.
The condition to prevent undercut in a spur gear is:
The number of teeth without undercut will be:
The coefficient without undercut is:
Profile shift is not merely used to prevent undercut. It can be used to adjust centre distance between two gears.
If a positive correction is applied, such as to prevent undercut in a pinion, the tooth thickness at top is thinner.
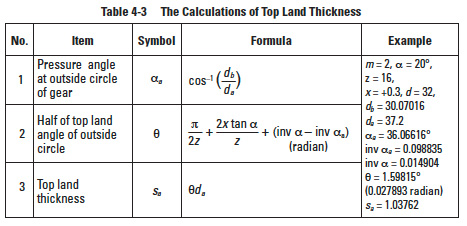
Table 4-3 presents the calculation of top land thickness.
4.6 Profile Shifted Spur GearEdit
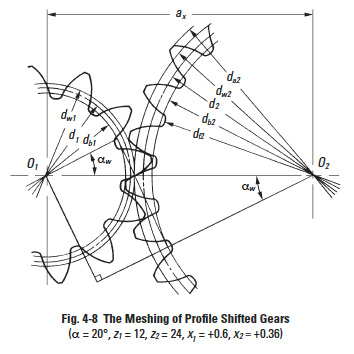
Figure 4-8 shows the meshing of a pair of profile shifted gears. The key items in profile shifted gears are the operating (working) pitch diameters (dw) and the working (operating) pressure angle (αw). These values are obtainable from the operating (or i.e., actual) centre distance and the following formulas:
In the meshing of profile shifted gears, it is the operating pitch circles that are in contact and roll on each other that portrays gear action. The standard pitch circles no longer are of significance; and the operating pressure angle is what matters.
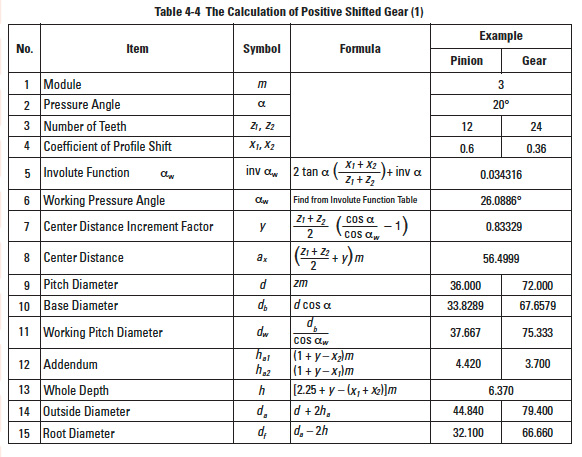
A standard spur gear is, according to Table 4-4, a profile shifted gear with 0 coefficient of shift; that is, x1 = x2 = 0. Table 4-5 is the inverse formula of items from 4 to 8 of Table 4-4.
There are several theories concerning how to distribute the sum of coefficient of profile shift, (x1 + x2) into pinion, (x1) and gear, (x2) separately. BSS (British) and DIN (German) standards are the most often used. In the example above, the 12 tooth pinion was given sufficient correction to prevent undercut, and the residual profile shift was given to the mating gear.
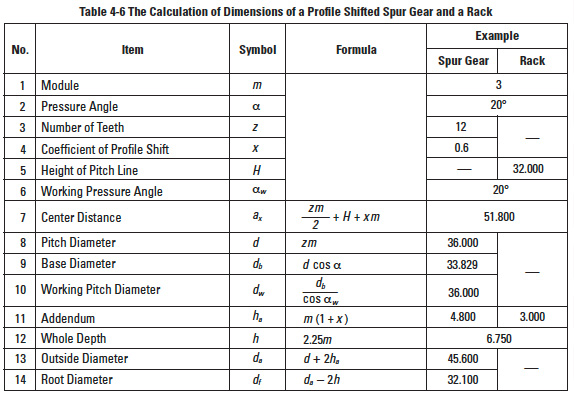
4.7 Rack And Spur GearEdit
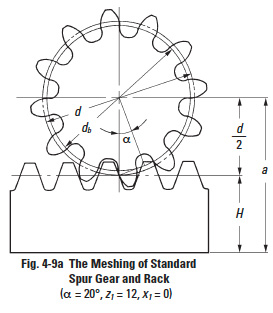
Table 4-6 presents the method for calculating the mesh of a rack and spur gear. Figure 4-9a shows the pitch circle of a standard gear and the pitch line of the rack.
One rotation of the spur gear will displace the rack (l) one circumferential length of the gear's pitch circle, per the formula:
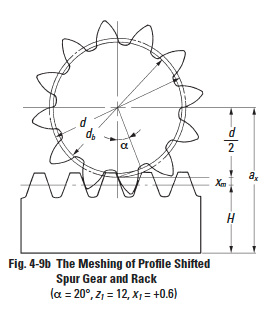
Figure 4-9b shows a profile shifted spur gear, with positive correction xm, meshed with a rack. The spur gear has a larger pitch radius than standard, by the amount xm. Also, the pitch line of the rack has shifted outward by the amount xm. Table 4-6 presents the calculation of a meshed profile shifted spur gear and rack. If the correction factor x1 is 0, then it is the case of a standard gear meshed with the rack. The rack displacement, l, is not changed in any way by the profile shifting. Equation (4-6) remains applicable for any amount of profile shift.