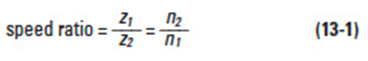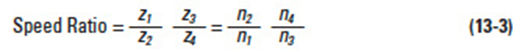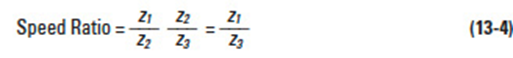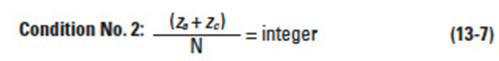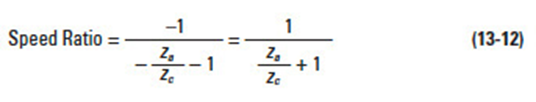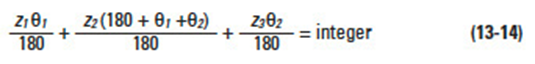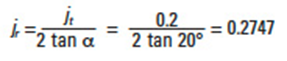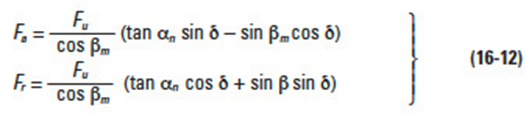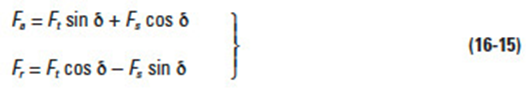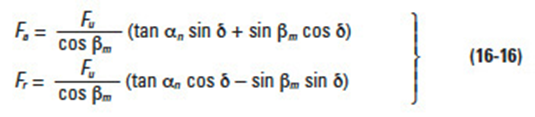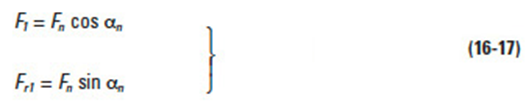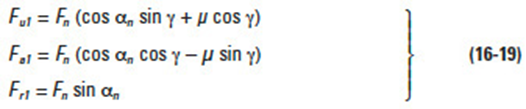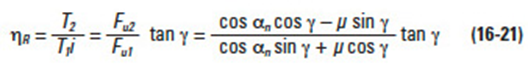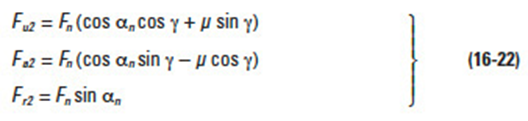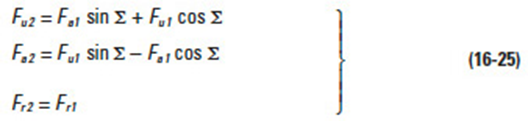Gears sections 13 - 16

Section 13: Gear Trains

The objective of gears is to provide a desired motion, either rotation or linear. This is accomplished through either a simple gear pair or a more involved and complex system of several gear meshes. Also, related to this is the desired speed, direction of rotation and the shaft arrangement.

13.1 Single-Stage Gear Train

A meshed gear is the basic form of a single stage gear train. It consists of z₁ and z₂ numbers of teeth on the driver and driven gears, and their respective rotations, n₁ & n₂. The speed ratio is then:

13.1.1 Types Of Single-Stage Gear Trains

Gear trains can be classified into three types:

1. Speed ratio > 1, increasing: n₁ < n₂
2. ratio = 1, equal speeds: n₁ = n₂
3. Speed ratio < 1, reducing: n₁ > n₂

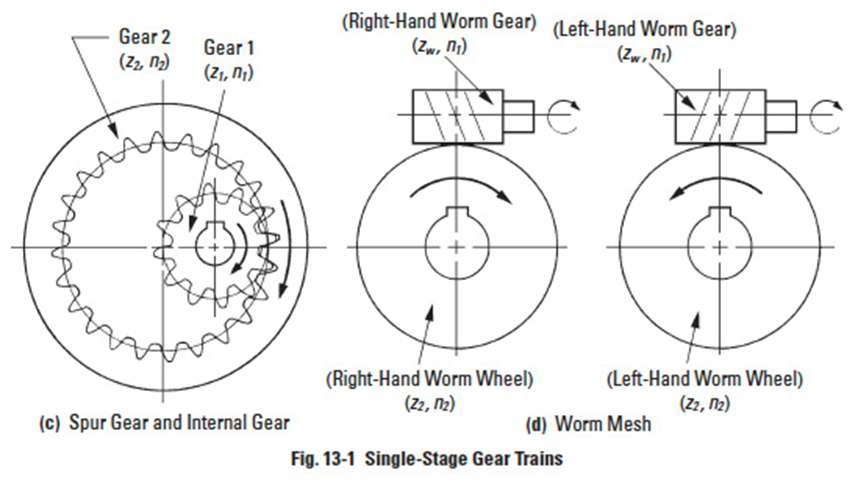
Figure 13-1

Figure 13-1a

Figure 13-1b

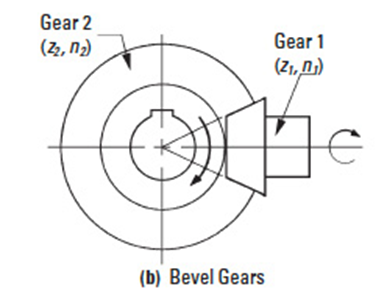
Figure 13-1 illustrates four basic types. For the very common cases of spur and bevel meshes, Figures 13-1(a) and 13-1(b), the direction of rotation of driver and driven gears are reversed. In the case of an internal gear mesh, Figure 13-1(c), both gears have the same direction of rotation. In the case of a worm mesh, Figure 13-1(d), the rotation direction of z₂ is determined by its helix hand.

In addition to these four basic forms, the combination of a rack and gear can be considered a specific type. The displacement of a rack, l, for rotation θ of the mating gear is:

where:

π_m is the standard circular pitch

z₁ is the number of teeth of the gear

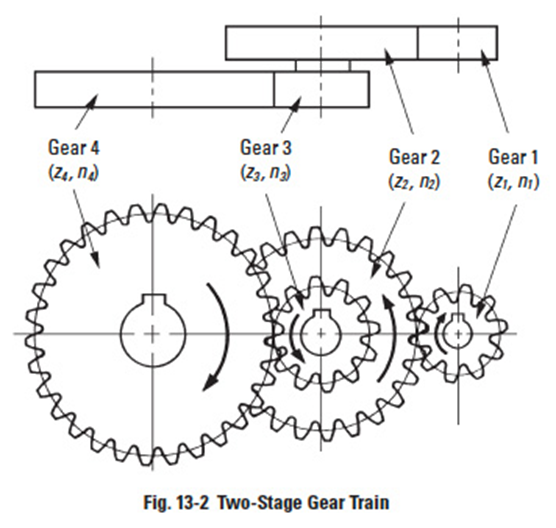
Figure 13-2

Figure 13-3

13.2 Two-Stage Gear Train

A two-stage gear train uses two single-stages in a series. Figure 13-2 represents the basic form of an external gear two-stage gear train.

Let the first gear in the first stage be the driver. Then the speed ratio of the two-stage train is:

In this arrangement, n₂ = n₃

In the two-stage gear train, Figure 13-2, gear 1 rotates in the same direction as gear 4. If gears 2 and 3 have the same number of teeth, then the train simplifies as in Figure 13-3. In this arrangement, gear 2 is known as an idler, which has no effect on the gear ratio. The speed ratio is then:

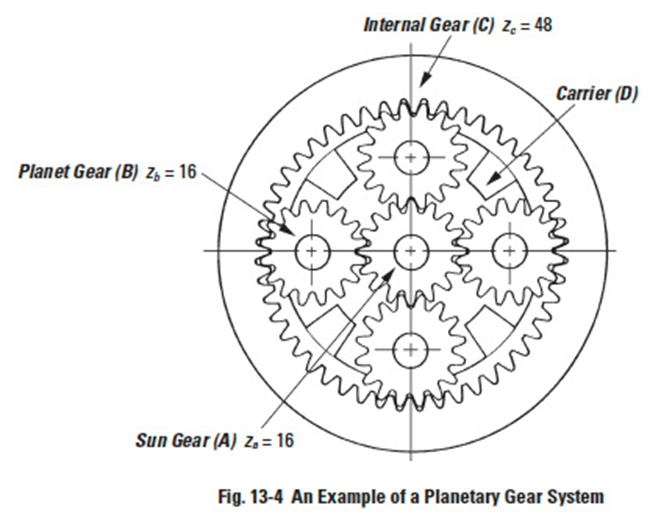
Figure 13-4

13.3 Planetary Gear System

The basic form of a planetary gear system is shown in Figure 13-4. It consists of a Sun Gear (A), Planet Gears (B), Internal Gear (C) and Carrier (D). The input and output axes of a planetary gear system are on a same line. Usually, it uses two or more planet gears to balance the load evenly. It is compact in space, but complex in structure. Planetary gear systems need a high-quality manufacturing process. The load division between planet gears, the interference of the internal gear, the balance and vibration of the rotating carrier, and the hazard of jamming, etc. are inherent problems to be solved.

Figure 13-4 is a so called 2K-H type planetary gear system. The sun gear, internal gear, and the carrier have a common axis.

13.3.1 Relationship Among The Gears In A Planetary Gear System

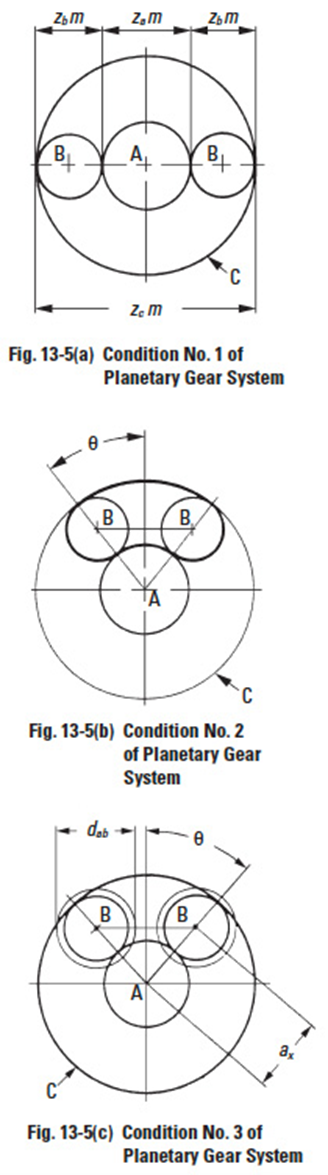
In order to determine the relationship among the numbers of teeth of the sun gear A, (z_a), the planet gears B, (z_b), and the internal gear C, (z_c), and the number of planet gears, N, in the system, the parameters must satisfy the following three conditions:

This is the condition necessary for the center distances of the gears to match. Since the equation is true only for the standard gear system, it is possible to vary the numbers of teeth by using profile shifted gear designs.

To use profile shifted gears, it is necessary to match the center distance between the sun A and planet B gears, a_x1, and the center distance between the planet B and internal C gears, a_x2.

This is the condition necessary for placing planet gears evenly spaced around the sun gear. If an uneven placement of planet gears is desired, then Equation (13-8) must be satisfied.

where:

θ = half the angle between adjacent planet gears

Condition No. 3:

Satisfying this condition insures that adjacent planet gears can operate without interfering with each other. This is the condition that must be met for standard gear design with equal placement of planet gears. For other conditions, the system must satisfy the relationship:

where:

d_ab = outside diameter of the planet gears

a_x = center distance between the sun and planet gears

Besides the above three basic conditions, there can be an interference problem between the internal gear C and the planet gears B. See SECTION 5 that discusses more about this problem.

Figure 13-6a

Figure 13-6b

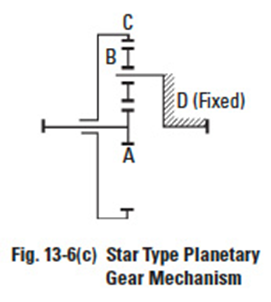
Figure 13-6c

13.3.2 Speed Ratio Of Planetary Gear System

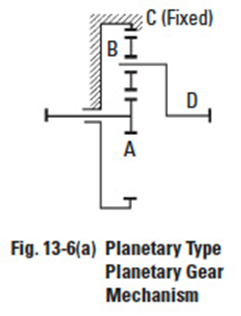
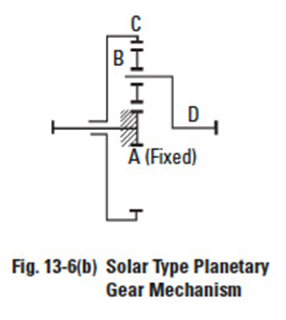
In a planetary gear system, the speed ratio and the direction of rotation would be changed according to which member is fixed. Figures 13-6(a), 13-6(b) and 13-6(c) contain three typical types of planetary gear mechanisms, depending upon which member is locked.

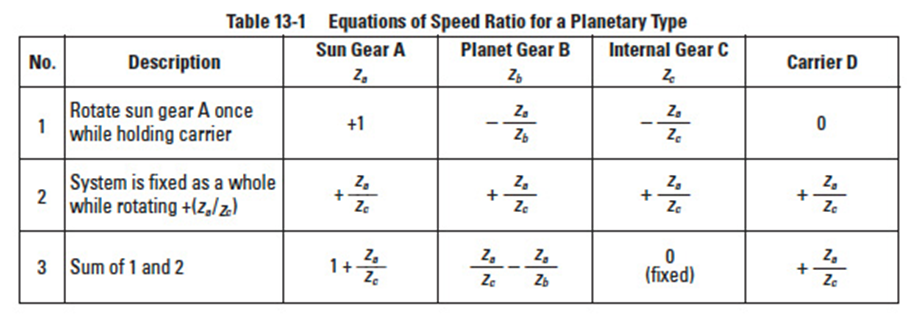
Table 13-1

(a) Planetary Type

In this type, the internal gear is fixed. The input is the sun gear and the output is carrier D. The speed ratio is calculated as in Table 13-1.

Note that the direction of rotation of input and output axes are the same. Example: z_a = 16, z_b = 16, z_c = 48, then speed ratio = 1/4.

(b) Solar Type

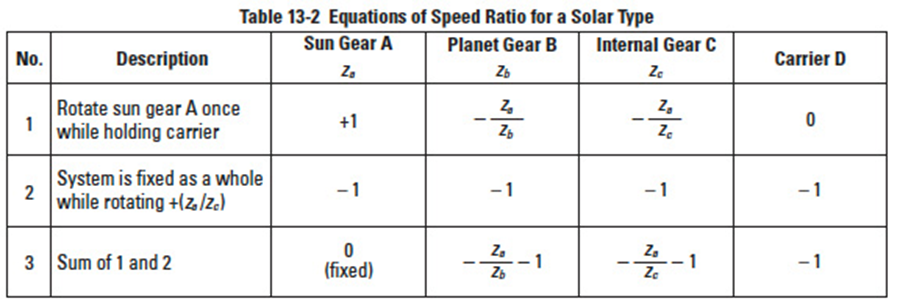
Table 13-2

In this type, the sun gear is fixed. The internal gear C is the input, and carrier D axis is the output. The speed ratio is calculated as in Table 13-2, on the following page.

Note that the directions of rotation of input and output axes are the same.

Example: z_a = 16, z_b = 16, z_c = 48, then the speed ratio = 1/1.3333333.

(c) Star Type

This is the type in which Carrier D is fixed. The planet gears B rotate only on fixed axes. In a strict definition, this train loses the features of a planetary system and it becomes an ordinary gear train. The sun gear is an input axis and the internal gear is the output. The speed ratio is:

Figure 13-6c

Referring to Figure 13-6(c), the planet gears are merely idlers. Input and output axes have opposite rotations.

Example: z_a = 16, z_b = 16, z_c = 48; then speed ratio = –1/3.

Figure 13-5

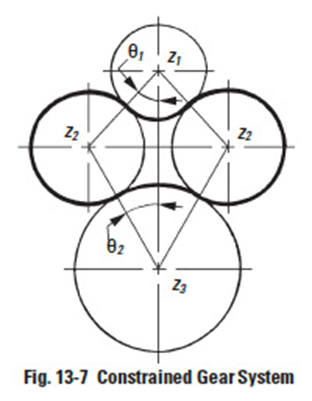
13.4 Constrained Gear System

A planetary gear system which has four gears, as in Figure 13-5, is an example of a constrained gear system. It is a closed loop system in which the power is transmitted from the driving gear through other gears and eventually to the driven gear. A closed loop gear system will not work if the gears do not meet specific conditions.

Figure 13-7

Let z₁, z₂ and z₃ be the numbers of gear teeth, as in Figure 13-7. Meshing cannot function if the length of the heavy line (belt) does not divide evenly by circular pitch. Equation (13-14) defines this condition.

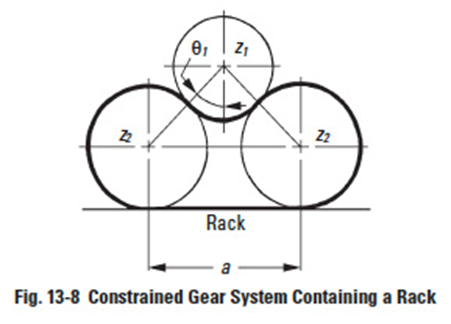
Figure 13-8

Figure 13-8 shows a constrained gear system in which a rack is meshed. The heavy line in Figure 13-8 corresponds to the belt in Figure 13-7. If the length of the belt cannot be evenly divided by circular pitch then the system does not work. It is described by Equation (13-15).

Section 14: Backlash

Up to this point the discussion has implied that there is no backlash. If the gears are of standard tooth proportion design and operate on standard center distance they would function ideally with neither backlash nor jamming.

Backlash is provided for a variety of reasons and cannot be designated without consideration of machining conditions. The general purpose of backlash is to prevent gears from jamming by making contact on both sides of their teeth simultaneously. A small amount of backlash is also desirable to provide for lubricant space and differential expansion between the gear components and the housing. Any error in machining which tends to increase the possibility of jamming makes it necessary to increase the amount of backlash by at least as much as the possible cumulative errors. Consequently, the smaller the amount of backlash, the more accurate must be the machining of the gears. Runout of both gears, errors in profile, pitch, tooth thickness, helix angle and center distance – all are factors to consider in the specification of the amount of backlash. On the other hand, excessive backlash is objectionable, particularly if the drive is frequently reversing or if there is an overrunning load. The amount of backlash must not be excessive for the requirements of the job, but it should be sufficient so that machining costs are not higher than necessary.

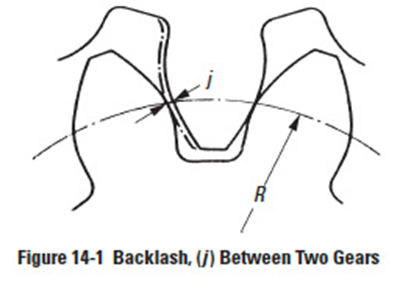
In order to obtain the amount of backlash desired, it is necessary to decrease tooth thickness. See Figure 14-1. This decrease must almost always be greater than the desired backlash because of the errors in manufacturing and assembling. Since the amount of the decrease in tooth thickness depends upon the accuracy of machining, the allowance for a specified backlash will vary according to the manufacturing conditions.

It is customary to make half of the allowance for backlash on the tooth thickness of each gear of a pair, although there are exceptions. For example, on pinions having very low numbers of teeth, it is desirable to provide all of the allowance on the mating gear so as not to weaken the pinion teeth.

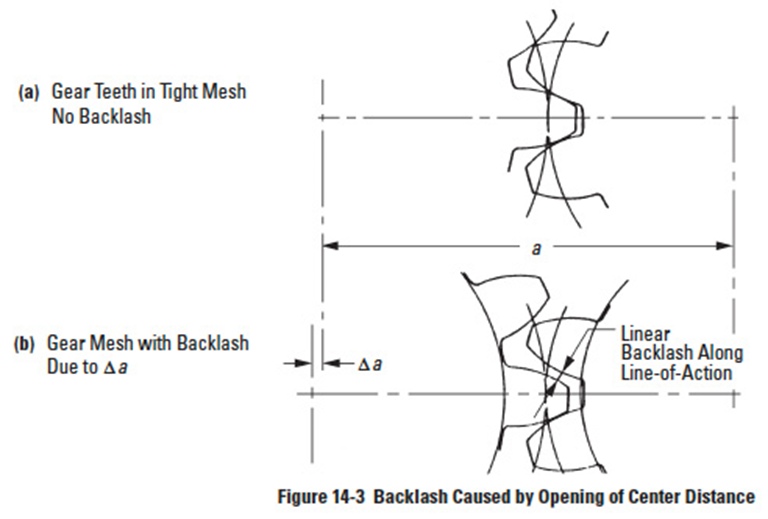
In spur and helical gearing, backlash allowance is usually obtained by sinking the hob deeper into the blank than the theoretically standard depth. Further, it is true that any increase or decrease in center distance of two gears in any mesh will cause an increase or decrease in backlash. Thus, this is an alternate way of designing backlash into the system.

In the following, we give the fundamental equations for the determination of backlash in a single gear mesh. For the determination of backlash in gear trains, it is necessary to sum the backlash of each mated gear pair. However, to obtain the total backlash for a series of meshes, it is necessary to take into account the gear ratio of each mesh relative to a chosen reference shaft in the gear train. For details, see Reference 10 at the end of the technical section.

Figure 14-1

14.1 Definition Of Backlash

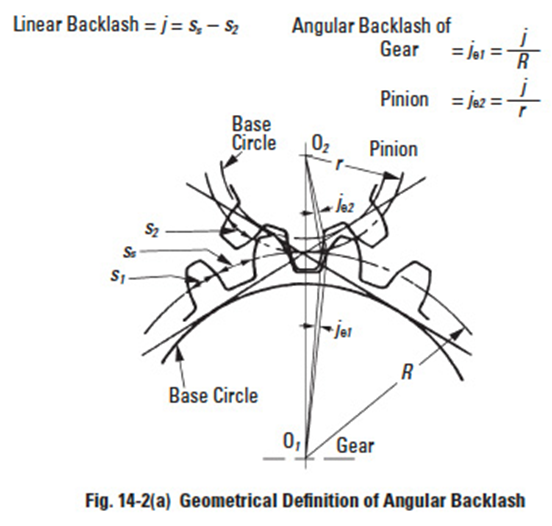
Figure 14-2a

Backlash is defined in Figure 14-2(a) as the excess thickness of tooth space over the thickness of the mating tooth. There are two basic ways in which backlash arises: tooth thickness is below the zero backlash value; and the operating center distance is greater than the zero backlash value.

If the tooth thickness of either or both mating gears is less than the zero backlash value, the amount of backlash introduced in the mesh is simply this numerical difference:

Figure 14-2b

Figure 14-3

where:

j = linear backlash measured along the pitch circle (Figure 14-2(b))

s_std = no backlash tooth thickness on the operating pitch circle, which is the standard tooth thickness for ideal gears

s_act = actual tooth thickness

When the center distance is increased by a relatively small amount, Δa, a backlash space develops between mating teeth, as in Figure 14-3. The relationship between center distance increase and linear backlash j_n along the line-of-action is:

This measure along the line-of-action is useful when inserting a feeler gage between teeth to measure backlash. The equivalent linear backlash measured along the pitch circle is given by:

where:

Δ a = change in center distance

α = pressure angle

Hence, an approximate relationship between center distance change and change in backlash is:

Although these are approximate relationships, they are adequate for most uses. Their derivation, limitations, and correction factors are detailed in Reference 10.

Note that backlash due to center distance opening is dependent upon the tangent function of the pressure angle. Thus, 20° gears have 41° more backlash than 14.5° gears, and this constitutes one of the few advantages of the lower pressure angle.

Equations (14-3) are a useful relationship, particularly for converting to angular backlash. Also, for fine pitch gears the use of feeler gages for measurement is impractical, whereas an indicator at the pitch line gives a direct measure. The two linear backlashes are related by:

The angular backlash at the gear shaft is usually the critical factor in the gear application. As seen from Figure 14-2(a), this is related to the gear's pitch radius as follows:

Obviously, angular backlash is inversely proportional to gear radius. Also, since the two meshing gears are usually of different pitch diameters, the linear backlash of the measure converts to different angular values for each gear. Thus, an angular backlash must be specified with reference to a particular shaft or gear center.

Details of backlash calculations and formulas for various gear types are given in the following sections.

14.2 Backlash Relationships

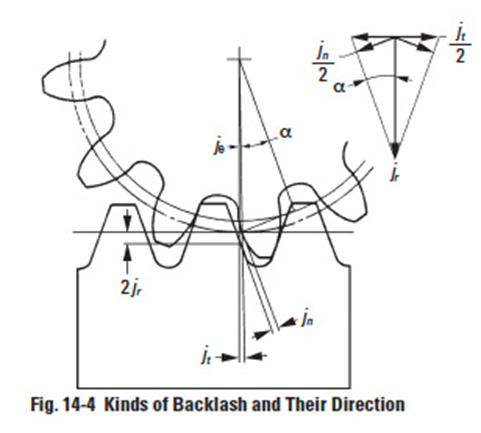
'Figure 14-4

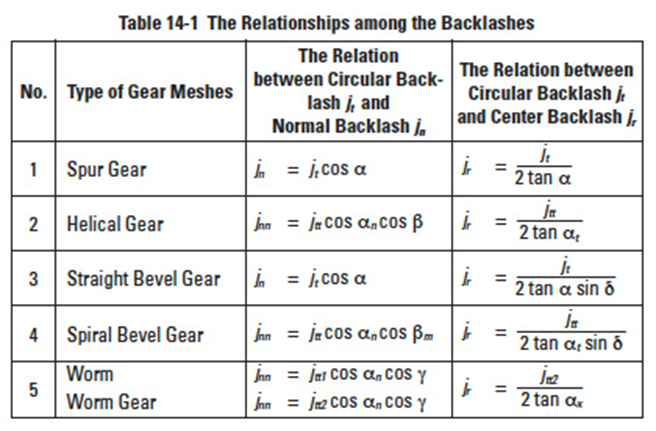
Table 14-1

Expanding upon the previous definition, there are several kinds of backlash: circular backlash j_t, normal backlash j_n, center backlash j_r , and angular backlash Jθ (°), see Figure 14-4.

Table 14-1 reveals relationships among circular backlash j_t, normal backlash j_n and center backlash j_r. In this definition, j_r is equivalent to change in center distance, Δa, in Section 14.1.

Circular backlash j_t has a relation with angular backlash jθ, as follows:

14.2.1 Backlash Of A Spur Gear Mesh

From Figure 14-4 we can derive backlash of spur mesh as:  

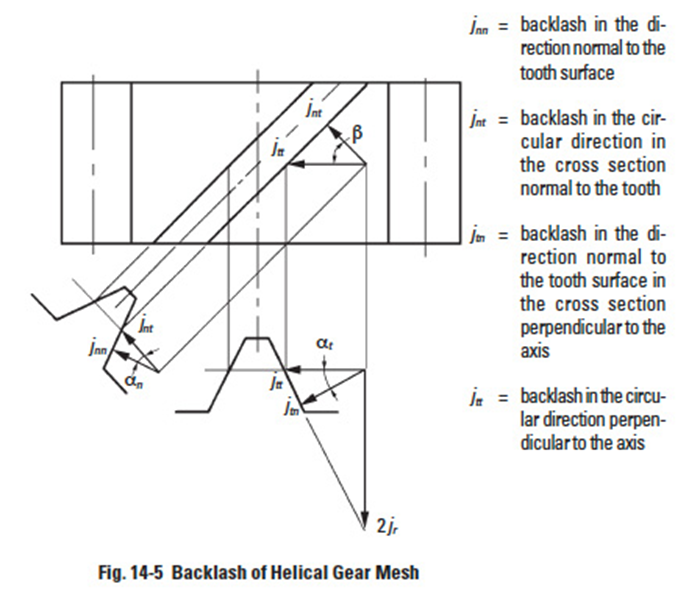
14.2.2 Backlash Of Helical Gear Mesh

The helical gear has two kinds of backlash when referring to the tooth space. There is a cross section in the normal direction of the tooth surface n, and a cross section in the radial direction perpendicular to the axis, t.

These backlashes have relations as follows:

In the plane normal to the tooth:

On the pitch surface:

In the plane perpendicular to the axis:

Figure 14-6

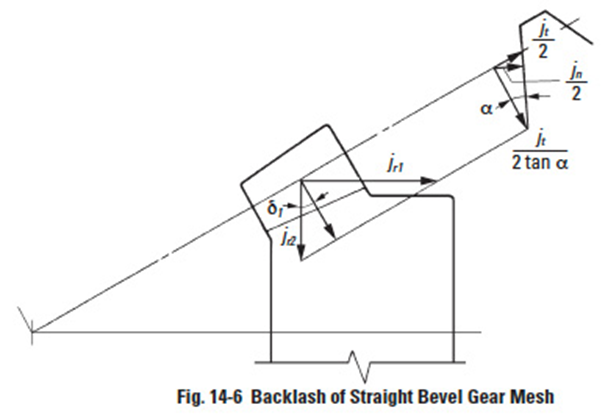
14.2.3 Backlash Of Straight Bevel Gear Mesh

Figure 14-6 expresses backlash for a straight bevel gear mesh.

In the cross section perpendicular to the tooth of a straight bevel gear, circular backlash at pitch line j_t, normal backlash j_n and radial backlash j_r' have the following relationships:

The radial backlash in the plane of axes can be broken down into the components in the direction of bevel pinion center axis, j_r1, and in the direction of bevel gear center axis, j_r2.  

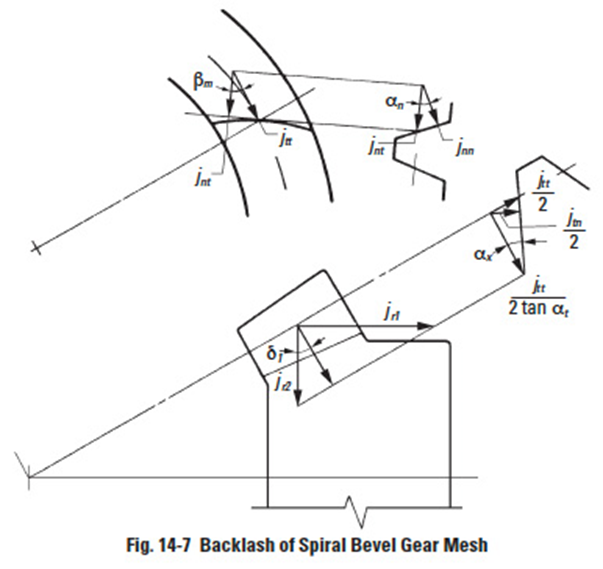
14.2.4 Backlash Of A Spiral Bevel Gear Mesh

Figure 14-7 delineates backlash for a spiral bevel gear mesh.

Figure 14-7

In the tooth space cross section normal to the tooth:

On the pitch surface:

In the plane perpendicular to the generatrix of the pitch cone:

The radial backlash in the plane of axes can be broken down into the components in the direction of bevel pinion center axis, j_r1, and in the direction of bevel gear center axis, j_r2.

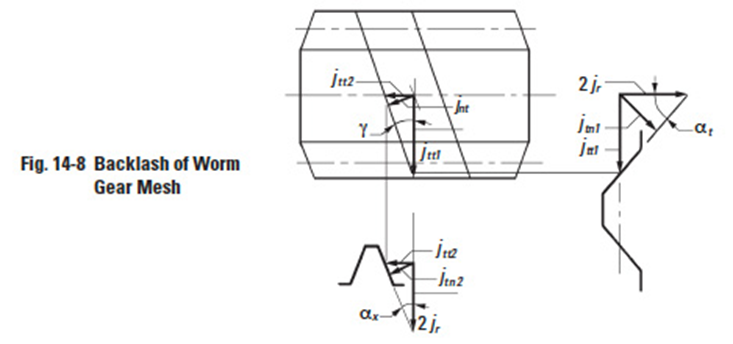
Figure 14-8

14.2.5 Backlash Of Worm Gear Mesh

Figure 14-8 expresses backlash for a worm gear mesh.

On the pitch surface of a worm:

In the cross section of a worm perpendicular to its axis:

In the plane perpendicular to the axis of the worm gear:

14.3 Tooth Thickness And Backlash

There are two ways to produce backlash. One is to enlarge the center distance. The other is to reduce the tooth thickness. The latter is much more popular than the former. We are going to discuss more about the way of reducing the tooth thickness. In SECTION 10, we have discussed the standard tooth thickness s. In the meshing of a pair of gears, if the tooth thickness of pinion and gear were reduced by Δs₁ and Δs₂, they would generate a backlash of Δs₁ + Δs₂ in the direction of the pitchcircle.

Let the magnitude of Δs₁, Δs₂ be 0.1. We know that α = 20°, then:

j_t = Δs₁ + Δs₂ = 0.1 + 0.1 = 0.2 We can convert it into the backlash on normal direction:

j_n = j_t cos α = 0.2 cos 20° = 0.1879

Let the backlash on the center distance direction be j_r, then:

They express the relationship among several kinds of backlashes. In application, one should consult the JIS standard.

There are two JIS standards for backlash – one is JIS B 1703-76 for spur gears and helical gears, and the other is JIS B 1705-73 for bevel gears. All these standards regulate the standard backlashes in the direction of the pitch circle j_t or j_tt. These standards can be applied directly, but the backlash beyond the standards may also be used for special purposes. When writing tooth thicknesses on a drawing, it is necessary to specify, in addition, the tolerances on the thicknesses as well as the backlash. For example:

Backlash 0.100 ... 0.200

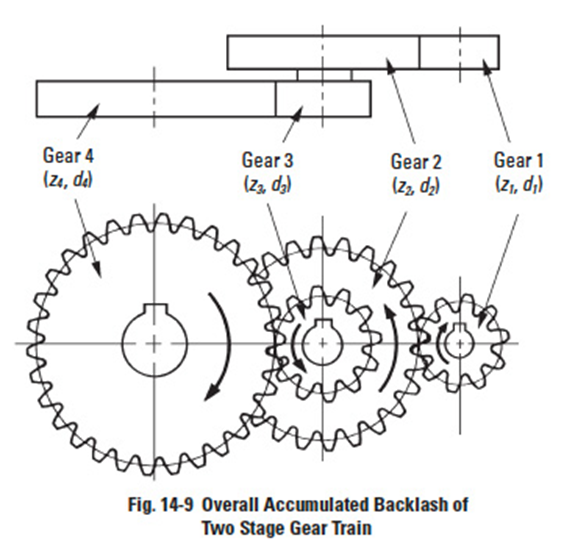
Figure 14-9

14.4 Gear Train And Backlash

The discussions so far involved a single pair of gears. Now, we are going to discuss two stage gear trains and their backlash. In a two stage gear train, as Figure 14-9 shows, j₁ and j₄ represent the backlashes of first stage gear train and second stage gear train respectively. If number one gear were fixed, then the accumulated backlash on number four gear j_tT4 would be as follows:

This accumulated backlash can be converted into rotation in degrees:

The reverse case is to fix number four gear and to examine the accumulated backlash on number one gear j_tT1.

This accumulated backlash can be converted into rotation in degrees:

14.5 Methods Of Controlling Backlash

In order to meet special needs, precision gears are used more frequently than ever before. Reducing backlash becomes an important issue. There are two methods of reducing or eliminating backlash – one a static, and the other a dynamic method.

The static method concerns means of assembling gears and then making proper adjustments to achieve the desired low backlash. The dynamic method introduces an external force which continually eliminates all backlash regardless of rotational position.

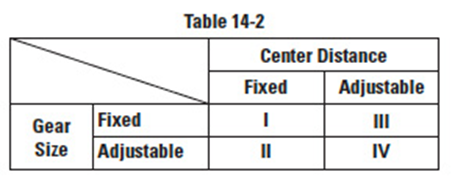
14.5.1 Static Method

This involves adjustment of either the gear's effective tooth thickness or the mesh center distance. These two independent adjustments can be used to produce four possible combinations as shown in Table 14-2.

Case I

By design, center distance and tooth thickness are such that they yield the proper amount of desired minimum backlash. Center distance and tooth thickness size are fixed at correct values and require precision manufacturing.

Case II

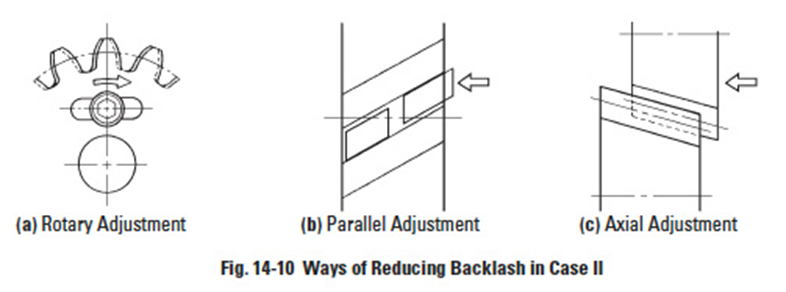
With gears mounted on fixed centers, adjustment is made to the effective tooth thickness by axial movement or other means. Three main methods are:

1. Two identical gears are mounted so that one can be rotated relative to the other and fixed. See Figure 14-10a. In this way, the effective tooth thickness can be adjusted to yield the desired low backlash.
2. A gear with a helix angle such as a helical gear is made in two half thicknesses. One is shifted axially such that each makes contact with the mating gear on the opposite sides of the tooth. See Figure 14-10b.
3. The backlash of cone shaped gears, such as bevel and tapered tooth spur gears, can be adjusted with axial positioning. A duplex lead worm can be adjusted similarly. See Figure 14-10c.

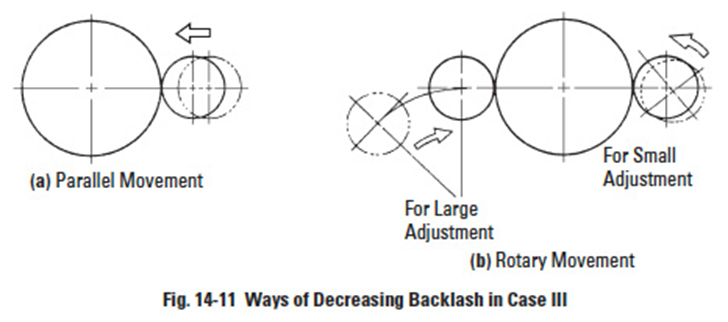
Case III

Center distance adjustment of backlash can be accomplished in two ways:

Linear Movement – Figure 14-11a shows adjustment along the line-of-centers in a straight or parallel axes manner. After setting to the desired value of backlash, the centers are locked in place.

1. Rotary Movement – Figure 14-11b shows an alternate way of achieving center distance adjustment by rotation of one of the gear centers by means of a swing arm on an eccentric bushing. Again, once the desired backlash setting is found, the positioning arm is locked.

Case IV

Adjustment of both center distance and tooth thickness is theoretically valid, but is not the usual practice. This would call for needless fabrication expense.

14.5.2 Dynamic Methods

Dynamic methods relate to the static techniques. However, they involve a forced adjustment of either the effective tooth thickness or the center distance.

1. Backlash Removal by Forced Tooth Contact
2. This is derived from static Case II. Referring to Figure 14-10a, a forcing spring rotates the two gear halves apart. This results in an effective tooth thickness that continually fills the entire tooth space in all mesh positions.
3. Backlash Removal by Forced Center Distance Closing
4. This is derived from static Case III. A spring force is applied to close the center distance; in one case as a linear force along the line-of-centers, and in the other case as a torque applied to the swing arm.

In all of these dynamic methods, the applied external force should be known and properly specified. The theoretical relationship of the forces involved is as follows:

where:

F₁ = Transmission Load on Tooth Surface

F₂ = Friction Force on Tooth Surface

If F < F₁ + F₂, then it would be impossible to remove backlash. But if F is excessively greater than a proper level, the tooth surfaces would be needlessly loaded and could lead to premature wear and shortened life. Thus, in designing such gears, consideration must be given to not only the needed transmission load, but also the forces acting upon the tooth surfaces caused by the spring load. It is important to appreciate that the spring loading must be set to accommodate the largest expected transmission force, F₁, and this maximum spring force is applied to the tooth surfaces continually and irrespective of the load being driven.

Figure 14-12

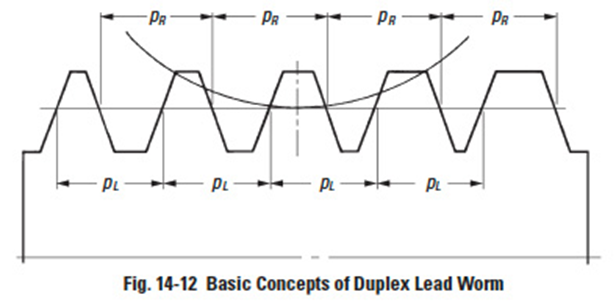
1. Duplex Lead Worm
2. A duplex lead worm mesh is a special design in which backlash can be adjusted by shifting the worm axially. It is useful for worm drives in high precision turntables and hobbing machines. Figure 14-12 presents the basic concept of a duplex lead worm.

The lead or pitch, p_L and p_R, on the two sides of the worm thread are not identical. The example in Figure 14-12 shows the case when p_R > p_L. To produce such a worm requires a special dual lead hob.

The intent of Figure 14-12 is to indicate that the worm tooth thickness is progressively bigger towards the right end. Thus, it is convenient to adjust backlash by simply moving the duplex worm in the axial direction.

Section 15: Gear accuracy

Gears are one of the basic elements used to transmit power and position. As designers, we desire them to meet various demands:

1. Minimum size.
2. Maximum power capability.
3. Minimum noise (silent operation).
4. Accurate rotation/position.

To meet various levels of these demands requires appropriate degrees of gear accuracy. This involves several gear features.

15.1 Accuracy Of Spur And Helical Gears

This discussion of spur and helical gear accuracy is based upon JIS B 1702 standard. This specification describes 9 grades of gear accuracy – grouped from 0 through 8 – and four types of pitch errors:

·  Single pitch error.

·  Pitch variation error.

·  Accumulated pitch error.

·  Normal pitch error.

Single pitch error, pitch variation and accumulated pitch errors are closely related with each other.

15.1.1 Pitch Errors of Gear Teeth

1. Single Pitch Error (f_pt)
2. The deviation between actual measured pitch value between any adjacent tooth surface and theoretical circular pitch.
3. Pitch Variation Error (f_pu)
4. Actual pitch variation between any two adjacent teeth. In the ideal case, the pitch variation error will be zero.
5. Accumulated Pitch Error (F_p)
6. Difference between theoretical summation over any number of teeth interval, and summation of actual pitch measurement over the same interval.
7. Normal Pitch Error (f_pb)
8. It is the difference between theoretical normal pitch and its actual measured value.

The major element to influence the pitch errors is the runout of gear flank groove.

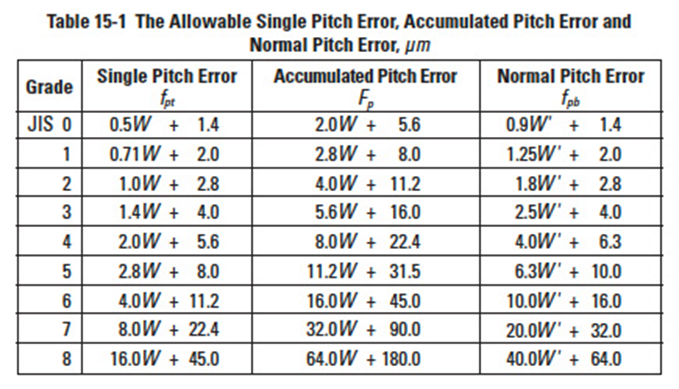
Table 15-1

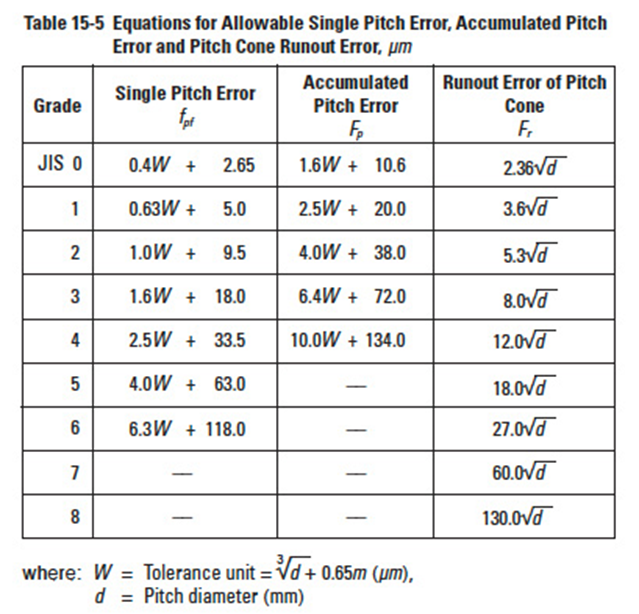
Table 15-1 contains the ranges of allowable pitch errors of spur gears and helical gears for each precision grade, as specified in JIS B 1702-1976.

In the above table, W and W' are the tolerance units defined as:

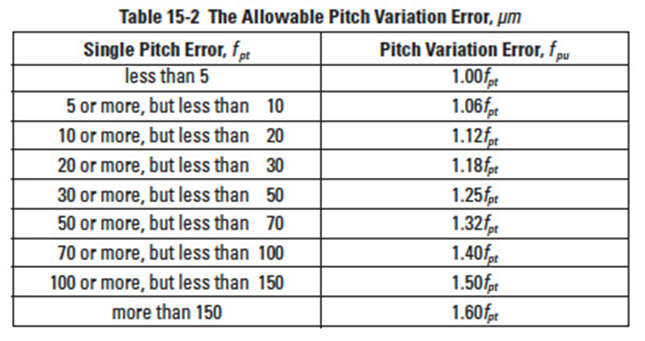
Table 15-2

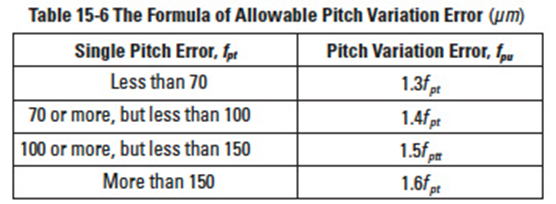
The value of allowable pitch variation error is k times the single pitch error. Table 15-2 expresses the formula of the allowable pitch variation error.

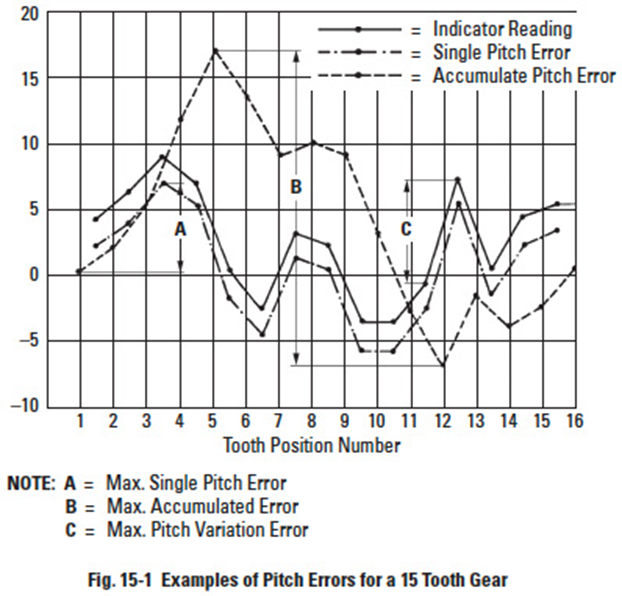
Figure 15-1 is an example of pitch errors derived from data measurements made with a dial indicator on a 15 tooth gear. Pitch differences were measured between adjacent teeth and are plotted in the figure. From that plot, single pitch, pitch variation and accumulated pitch errors are extracted and plotted.

Figure 15-1

15.1.2 Tooth Profile Error, f_f

Tooth profile error is the summation of deviation between actual tooth profile and correct involute curve which passes through the pitch point measured perpendicular to the actual profile. The measured band is the actual effective working surface of the gear. However, the tooth modification area is not considered as part of profile error.

15.1.3 Runout Error Of Gear Teeth, F_r

This error defines the runout of the pitch circle. It is the error in radial position of the teeth. Most often it is measured by indicating the position of a pin or ball inserted in each tooth space around the gear and taking the largest difference. Alternately, particularly for fine pitch gears, the gear is rolled with a master gear on a variable center distance fixture, which records the change in the center distance as the measure of teeth or pitch circle runout. Runout causes a number of problems, one of which is noise. The source of this error is most often insufficient accuracy and ruggedness of the cutting arbor and tooling system.

15.1.4 Lead Error, f_β

Lead error is the deviation of the actual advance of the tooth profile from the ideal value or position. Lead error results in poor tooth contact, particularly concentrating contact to the tip area. Modifications, such as tooth crowning and relieving can alleviate this error to some degree.

Figure 15-2

Table 15-3

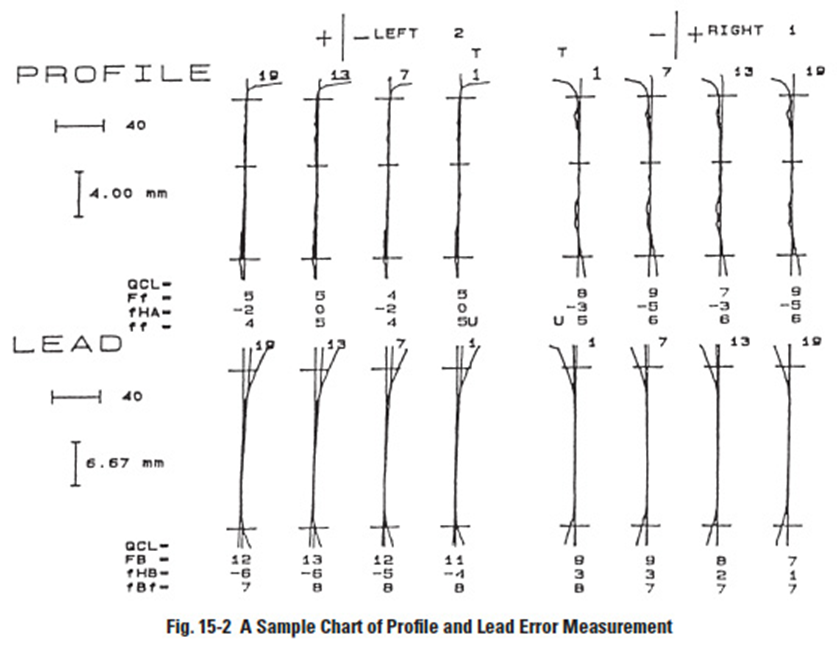
Shown in Figure 15-2 is an example of a chart measuring tooth profile error and lead error using a Zeiss UMC 550 tester. Also see Table 15-3.

15.1.5. Outside Diameter Runout and Lateral Runout

To produce a high precision gear requires starting with an accurate gear blank. Two criteria are very important:

1. Outside diameter (OD) runout.
2. Lateral (side face) runout.

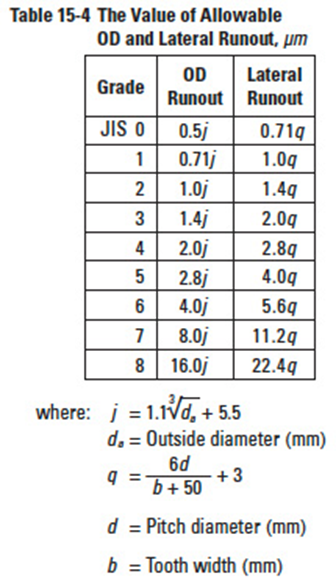
Table 15-4

The lateral runout has a large impact on the gear tooth accuracy. Generally, the permissible runout error is related to the gear size. Table 15-4 presents equations for allowable values of OD runout and lateral runout.

Table 15-5

15.2 Accuracy Of Bevel Gears

JIS B 1704 regulates the specification of a bevel gear's accuracy. It also groups bevel gears into 9 grades, from 0 to 8.

There are 4 types of allowable errors:

1. Single Pitch Error.
2. Pitch Variation Error.
3. Accumulated Pitch Error.
4. Runout Error of Teeth (pitch circle).

These are similar to the spur gear errors.

1. Single Pitch Error, (f_pt)
2. The deviation between actual measured pitch value between any adjacent teeth and the theoretical circular pitch at the central cone distance.
3. Pitch Variation Error, (f_pu)
4. Absolute pitch variation between any two adjacent teeth at the central cone distance.
5. Accumulated Pitch Error, (F_p)
6. Difference between theoretical pitch sum of any teeth interval, and the summation of actual measured pitches for the same teeth interval at the central cone distance.
7. Runout Error of Teeth, (F_r)
8. This is the maximum amount of tooth runout in the radial direction, measured by indicating a pin or ball placed between two teeth at the central cone distance. It is the pitch cone runout.

Table 15-5 presents equations for allowable values of these various errors.

Table 15-6

The equations of allowable pitch variations are in Table 15-6.

The equations of allowable pitch variations are in Table 15-6.

Besides the above errors, there are seven specifications for bevel gear blank dimensions and angles, plus an eighth that concerns the cut gear set:

1. The tolerance of the blank outside diameter and the crown to back surface distance.
2. The tolerance of the outer cone angle of the gear blank.
3. The tolerance of the cone surface runout of the gear blank.
4. The tolerance of the side surface runout of the gear blank.
5. The feeler gauge size to check the flatness of blank back surface.
6. The tolerance of the shaft bore dimension deviation of the gear blank.
7. The contact band of the tooth mesh.

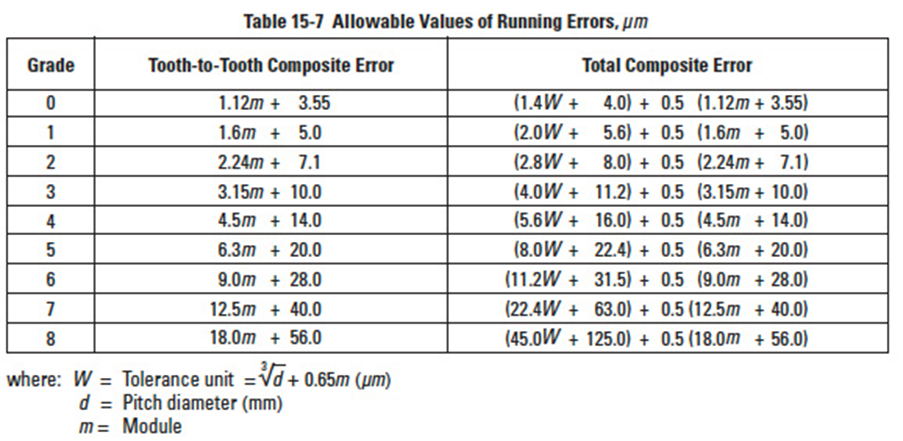
Table 15-7

Figure 15-

Item 8 relates to cutting of the two mating gears' teeth. The meshing tooth contact area must be full and even across the profiles. This is an important criterion that supersedes all other blank requirements.

15.3 Running (Dynamic) Gear Testing

An alternate simple means of testing the general accuracy of a gear is to rotate it with a mate, preferably of known high quality, and measure characteristics during rotation. This kind of tester can be either single contact (fixed center distance method) or dual (variable center distance method). This refers to action on one side or simultaneously on both sides of the tooth. This is also commonly referred to as single and double flank testing. Because of simplicity, dual contact testing is more popular than single contact. JGMA has a specification on accuracy of running tests.

1. Dual Contact (Double Flank) Testing
2. In this technique, the gear is forced meshed with a master gear such that there is intimate tooth contact on both sides and, therefore, no backlash. The contact is forced by a loading spring. As the gears rotate, there is variation of center distance due to various errors, most notably runout. This variation is measured and is a criterion of gear quality. A full rotation presents the total gear error, while rotation through one pitch is a tooth-to-tooth error. Figure 15-3 presents a typical plot for such a test.

For American engineers, this measurement test is identical to what AGMA designates as Total Composite Tolerance (or error) and Tooth-to-Tooth Composite Tolerance. Both of these parameters are also referred to in American publications as "errors", which they truly are. Tolerance is a design value which is an inaccurate description of the parameter, since it is an error. Allowable errors per JGMA 116-01 are presented on the next page, in Table 15-7.

1. Single Contact Testing
2. In this test, the gear is mated with a master gear on a fixed center distance and set in such a way that only one tooth side makes contact. The gears are rotated through this single flank contact action, and the angular transmission error of the driven gear is measured. This is a tedious testing method and is seldom used except for inspection of the very highest precision gears.

Section 16: Gear forces

In designing a gear, it is important to analyze the magnitude and direction of the forces acting upon the gear teeth, shaft, bearings, etc. In analyzing these forces, an idealized assumption is made that the tooth forces are acting upon the central part of the tooth flank.

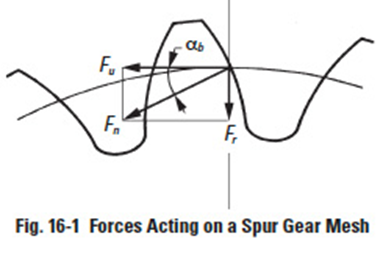
16.1 Forces In A Spur Gear Mesh

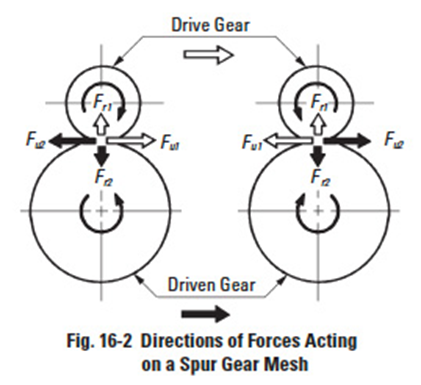
Figure 16-2

The spur gear's transmission force F_n, which is normal to the tooth surface, as in Figure 16-1, can be resolved into a tangential component, F_u, and a radial component, F_r. Refer to Equation (16-1). The direction of the forces acting on the gears are shown in Figure 16-2. The tangential component of the drive gear, F_u1, is equal to the driven gear's tangential component, F_u2, but the directions are opposite. Similarly, the same is true of the radial components.

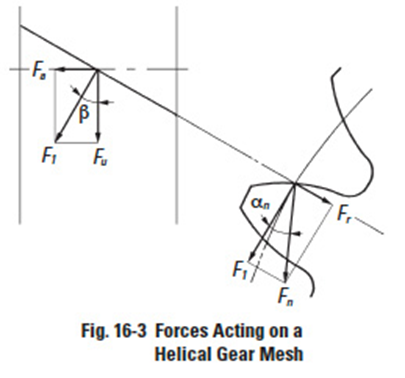
Figure 16-3

16.2 Forces In A Helical Gear Mesh

The helical gear's transmission force, F_n which is normal to the tooth surface, can be resolved into a tangential component, F₁, and a radial component, F_r. See Figure 16.3

The tangential component, F₁, can be further resolved into circular subcomponent, F_u, and axial thrust subcomponent, F_a.

Substituting and manipulating the above equations result in:

Figure 16-4

The directions of forces acting on a helical gear mesh are shown in Figure 16-4. The axial thrust sub-component from drive gear, F_a1, equals the driven gear's, F_a2, but their directions are opposite. Again, this case is the same as tangential components F_u1, F_u2 and radial components F_r1, F_r2.

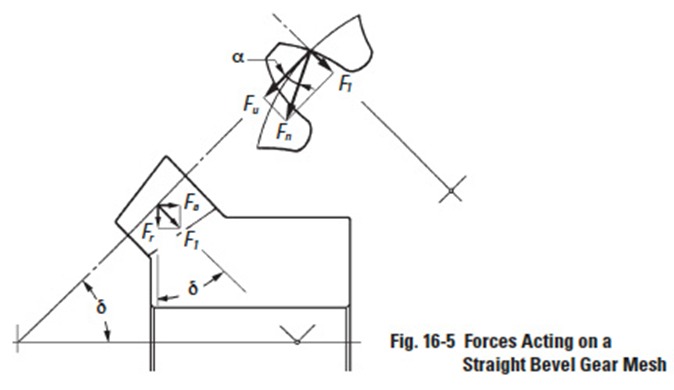
16.3 Forces On A Straight Bevel Gear Mesh

Figure 16-5

The forces acting on a straight bevel gear are shown in Figure 16-5. The force which is normal to the central part of the tooth face, F_n, can be split into tangential component, F_n, and radial component, F₁, in the normal plane of the tooth.

Again, the radial component, F₁, can be divided into an axial force, F_a, and a radial force,F_r, perpendicular to the axis.

And the following can be derived:

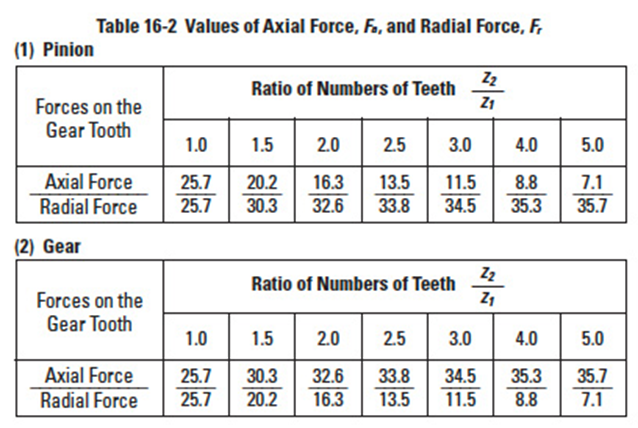
Table 16-2

Let a pair of straight bevel gears with a shaft angle Σ = 90°, a pressure angle α_n = 20° and tangential force, F_u, to the central part of tooth face be 100. Axial force, F_a, and radial force, F_r, will be as presented in Table 16-2.

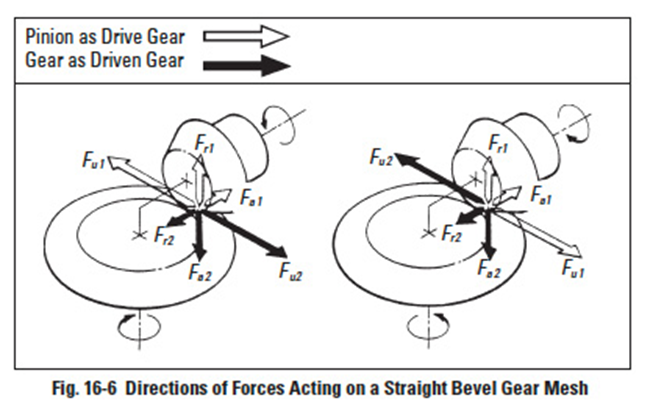
Figure 16-6

Figure 16-6 contains the directions of forces acting on a straight bevel gear mesh. In the meshing of a pair of straight bevel gears with shaft angle Σ = 90°, all the forces have relations as per Equations (16-8).

Figure 16-7

Table 16-3

16.4 Forces In A Spiral Bevel Gear Mesh

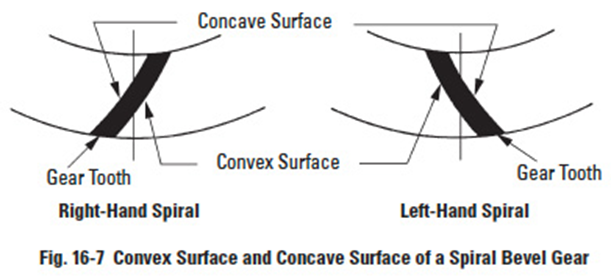
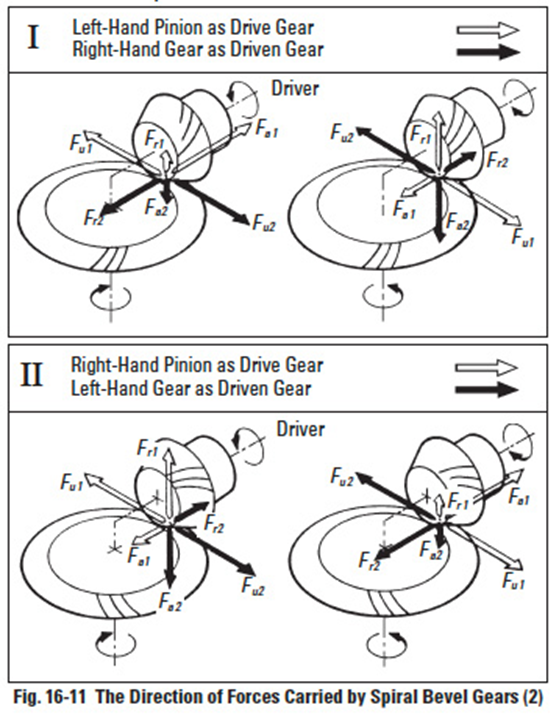
Spiral gear teeth have convex and concave sides. Depending on which surface the force is acting on, the direction and magnitude changes. They differ depending upon which is the driver and which is the driven. Figure 16-7 presents the profile orientations of righthand left-hand spiral teeth. If the profile of the driving gear is convex, then the profile of the driven gear must be concave. Table 16-3 presents the concave/convex relationships.

16.4.1 Tooth Forces On A Convex Side Profile

The transmission force, F_n, can be resolved into components F₁ and F_t as:

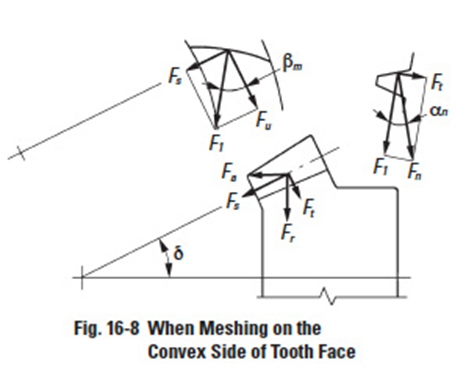
Figure 16-8

See Figure 16-8. Then F₁ can be resolved into components F_u and F_s:

On the axial surface, F_t and F_s can be resolved into axial and radial subcomponents.

By substitution and manipulation, we obtain:

Figure 16-9

16.4.2 Tooth Forces On A Concave Side Profile

On the surface which is normal to the tooth profile at the central portion of the tooth, the transmission force, F_n, can be split into F₁ and F_t as (see Figure 16-9):

And F₁ can be separated into components F_u and F_s on the pitch surface:

So far, the equations are identical to the convex case. However, differences exist in the signs for equation terms. On the axial surface, F_t and F_s can be resolved into axial and radial subcomponents. Note the sign differences.

The above can be manipulated to yield:

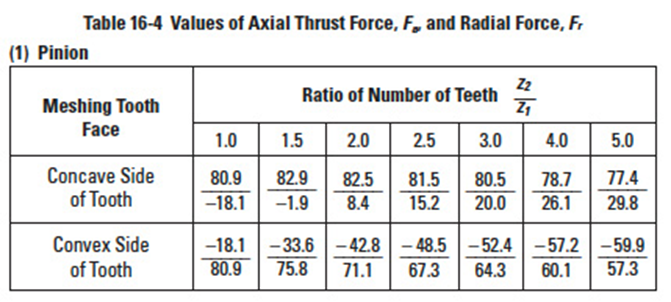
Table 16-4

Table 16-4 cont.

Let a pair of spiral bevel gears have a shaft angle Σ = 90°, a pressure angle α_n = 20°, and a spiral angle β_m = 35°. If the tangential force, F_u, to the central portion of the tooth face is 100, the axial thrust force, F_a, and radial force, F_r, have the relationship shown in Table 16-4, Table 16-4 (cont.)

The value of axial force, F_a, of a spiral bevel gear, from Table 16-4, could become negative. At that point, there are forces tending to push the two gears together. If there is any axial play in the bearing, it may lead to the undesirable condition of the mesh having no backlash. Therefore, it is important to pay particular attention to axial plays. From Table 16-4(2), we understand that axial thrust force, Fa, changes from positive to negative in the range of teeth ratio from 1.5 to 2.0 when a gear carries force on the convex side. The precise turning point of axial thrust force, F_a, is at the teeth ratio z₁ / z₂ = 1.57357.

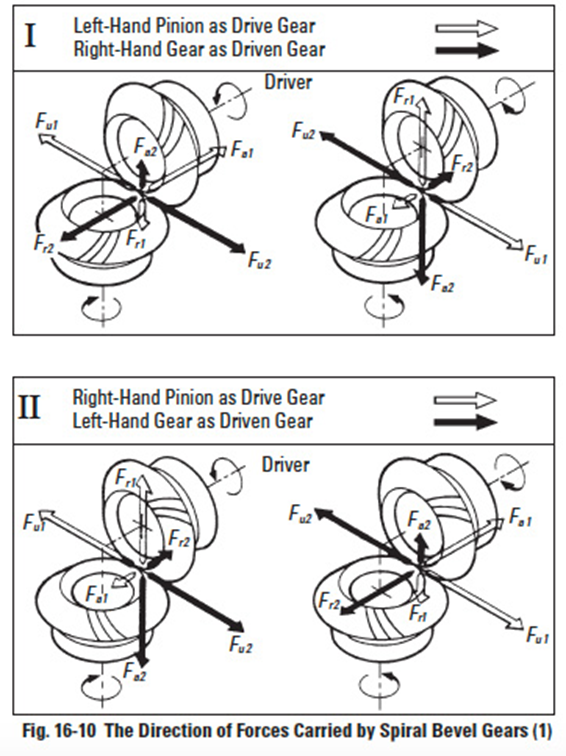
Figure 16-10

Figure 16-10 describes the forces for a pair of spiral bevel gears with shaft angle Σ = 90°, pressure angle α_n = 20°, spiral angle β_m = 35° and the teeth ratio, u, ranging from 1 to 1.57357.

Figure 16-11

Figure 16-11 expresses the forces of another pair of spiral bevel gears taken with the teeth ratio equal to or larger than 1.57357.

16.5 Forces In A Worm Gear Mesh

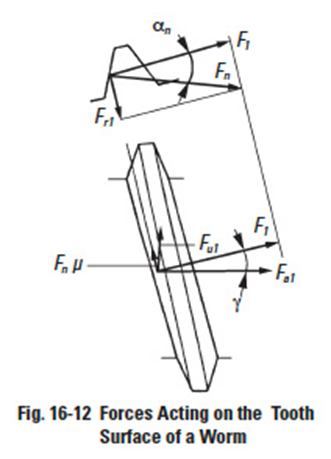
Figure 16-12

16.5.1 Worm as the Driver

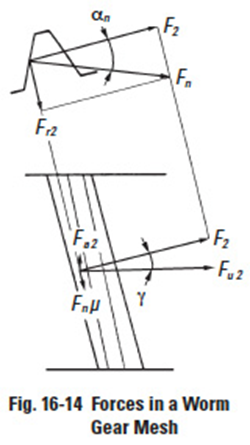
For the case of a worm as the driver, Figure 16-12, the transmission force, F_n, which is normal to the tooth surface at the pitch circle can be resolved into components F₁ and F_r1.

At the pitch surface of the worm, there is, in addition to the tangential component, F₁, a friction sliding force on the tooth surface, μF_n. These two forces can be resolved into the circular and axial directions as:

and by substitution, the result is:

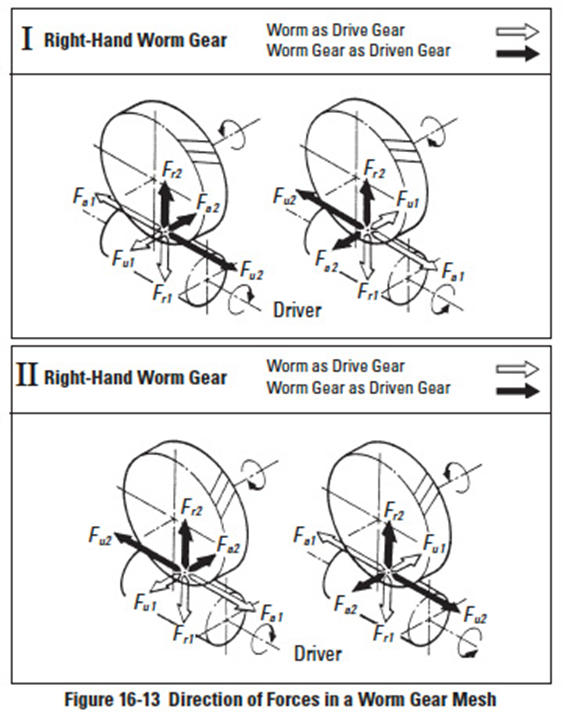
Figure 16-13

Figure 16-13 presents the direction of forces in a worm gear mesh with a shaft angle Σ = 90°. These forces relate as follows:

The coefficient of friction has a great effect on the transmission of a worm gear. Equation (16-21) presents the efficiency when the worm is the driver.

Figure 16-14

16.5.2 Worm Gear as the Driver

For the case of a worm gear as the driver, the forces are as in Figure 16-14 and per Equations (16-22).

When the worm and worm gear are at 90° shaft angle, Equations (16-20) apply. Then, when the worm gear is the driver, the transmission efficiency ηΙ is expressed as per Equation (16-23).

The equations concerning worm and worm gear forces contain the coefficient μ. This indicates the coefficient of friction is very important in the transmission of power.

16.6 Forces In A Screw Gear Mesh

The forces in a screw gear mesh are similar to those in a worm gear mesh. For screw gears that have a shaft angle Σ = 90°, merely replace the worm's lead angle γ, in Equation (16-22), with the screw gear's helix angle β₁.

Figure 16-15

In the general case when the shaft angle is not 90°, as in Figure 16-15, the driver screw gear has the same forces as for a worm mesh. These are expressed in Equations (16-24).

Forces acting on the driven gear can be calculated per Equations (16-25).

Figure 16-16

If the Σ term in Equation (16-25) is 90°, it becomes identical to Equation (16-20). Figure 16-16 presents the direction of forces in a screw gear mesh when the shaft angle Σ = 90° and β₁ = β₂ = 45°.